Otisni knjiguOtisni knjigu

Prikaz podataka u računalu

Sjedište: CARNET - Arhiva 2021 Loomen
E-kolegij: Pripreme za ispit iz informatike na državnoj maturi
Knjiga: Prikaz podataka u računalu
Otisnuo/la: Gost (anonimni korisnik)
Datum: nedjelja, 6. listopada 2024., 19:39

Opis

Prikaz brojeva i znakova u računalu

Sadržaj

1. Uvod

Uvod

Već znate kako su svi podaci u računalu prikazani kao niz bitova - u obliku nula i jedinica. Naučili ste i pretvarati dekadske brojeve u binarne. U ovoj ćemo lekciji prikaz brojeva i znakova u računalu prikazati malo detaljnije.

Krenut ćemo od najjednostavnijeg - prikaza cijelih brojeva, pa preko realnih do znakova.

Elemente u memoriji u koje se spremaju vrijednosti bitova nazivamo bistabili. Grupe bistabila nazivamo registar. U registru se nalazi 8, 16, 32 ili 64 bistabila, ovisno o  duljini riječi računala. Riječ je količina informacija koju računalo može obraditi u jednom periodu takta.

2. Prikaz cijelih brojeva metodom predznaka i apsolutne vrijednosti

Cijeli brojevi sastoje se od predznaka (+ ili -) i apsolutne vrijednosti broja. Na taj način ih možemo zapisati i u memoriju. S tom razlikom da i predznak moramo pohraniti kao binarni broj. Predznak "-" prikazat ćemo binarnom znamenkom 1, a predznak "+" binarnom znamenkom 0. Za zapis predznaka dovoljan je jedan bistabil. Zbog toga ćemo u registru zapisati cijeli broj na sljedeći način:

  • prvi bit rezerviran je za predznak, dok su preostali bitovi rezervirani za apsolutnu vrijednost broja. To znači da u 8-bitnom registru imamo 7 bitova za vrijednost broja, u 16-bitnom imamo 15, dok u 32-bitnom registru imamo na raspolaganju 31 bit za vrijednost broja.

Primjer 1:

Broj 27 zapisan u 8-bitnom registru:

Primjer1

Broj 27 jednostavno pretvorimo u binarni broj: (16+8+2+1) => 11011(2).
Prvi bit je bit za predznak, pa u prvi bistabil upisujemo nulu. Kako nam je ostalo još 7 "mjesta", a za broj 27 potrebno je samo 5, potrebno je dva bistabila s lijeve strane dopuniti nulama.

Zašto s lijeve?
Iz jednostavnog razloga - nule s lijeve strane ne mijenjaju vrijednost broja.

Zadatak:

Koji je najveći broj zapisan u 8-bitnom registru u zapisu pomoću predznaka i apsolutne vrijednosti?

Primjer 2:

Broj -27 zapisan u 8 bitnom registru pomoću predznaka i apsolutne vrijednosti:

Primjer 2

Zadatak 1:

Koji je najmanji broj zapisan u 8-bitnom registru u zapisu pomoću predznaka i apsolutne vrijednosti?

Zadatak 2:

Zapišite brojeve 134 i -134 u 16-bitnom registru.

Zadatak 3:

U 16-bitnom registru zapisan je sadržaj 1000000000011011. O kojem dekadskom broju se radi ako znamo da je to zapis cijelog broja pomoću predznaka i apsolutne vrijednosti.

2.1. Zadatci s provedenih ispita

  1. (2013, ljetni rok, zadatak 11) Za prikaz brojeva upotrebljava se registar duljine 1 B te metoda predznaka i apsolutne vrijednosti. Koji će biti prikaz broja -19?
    A. 00010011
    B. 10010011
    C. 11101100
    D. 11101101

  2. (2013, ljetni rok, zadatak 28) Koji se najveći cijeli broj (u dekadskome brojevnom sustavu) može zapisati u 8-bitovnome registru ako se za zapis cijeloga broja upotrebljava metoda predznaka i apsolutne vrijednosti?

  3. (2014, jesenski rok, zadatak 27) U 8-bitovnome registru zapisan je prirodni broj 180. Koji bi to cijeli broj bio ako bismo na sadržaj registra gledali kao na zapis cijeloga broja s predznakom i apsolutnom vrijednosti?

  4. (2015, ljetni rok, zadatak 11) Sadržaj 8-bitovnoga registra je 10010101. Koji je to dekadski broj ako je poznato da je u registru zapisan cijeli broj s predznakom i apsolutnom vrijednosti?
    A. –149
    B. –21
    C. 21
    D. 149

  5. (2016, ljetni rok, zadatak 27) Sadržaj 8-bitovnoga registra A jest 110011002, a radi se o binarnome zapisu vrijednosti cijeloga broja metodom predznaka i apsolutne vrijednosti. Dekadska vrijednost iz registra A, umanjena za jedan, pohranjena je istom metodom u registar B. Koji je binarni sadržaj registra B?

2.2. Rješenja

  1. B
  2. 127
  3. -52
  4. B
  5. 11001101

3. Prikaz cijelih brojeva metodom dvojnog komplementa

Osim zapisa s predznakom i apsolutnom vrijednošću broja, cijeli brojevi se u računalu zapisuju i pomoću dvojnog komplementa.

Kod ovog zapisa vodeći bit (koji predstavlja predznak broja) se u pretvorbi množi sa odgovarajućom težinskom vrijednosti, ali dobiva negativan predznak.

Primjer:

Broj -101 metodom dvojnog komplementa zapisan u 8-bitnom registru je:

Primjer 1

Kako možemo doći do tog zapisa?

Zapišimo najprije broj 101 u 8-bitnom registru. Kako je 101 = 64 + 32 +4 +1, zapis broja 101 u binarnom brojevnom sustavu je 1100101. Još trebamo dopuniti bit za predznak. Tako da je dekadski broj 101 zapisan u 8-bitnom registru 01100101.

Taj je zapis potpuno različit od zapisa -101. Kako ćemo sada doći do -101?

Postupak izračunavanja dvojnog komplementa binarnog broja je sljedeći:

  1. Izračunamo komplement binarnog broja. Komplement binarnog broja dobijemo tako da nule zamijenimo jedinicama, a jedinice nulama.
  2. Dobiveni komplement zbrojimo sa brojem 1.
  3. Tako dobiveni broj je dvojni komplement početnog binarnog broja, odnosno zapis negativnog broja.

Primjer:

Zapišimo sada dekadski broj -101 pomoću dvojnog komplementa. Broj 101 već smo pretvorili u binarni brojevni sustav i zapisali u 8-bitni registar:

Primjer 2

Zadatak 1:

Zapišite brojeve 57 i -57 u 8-bitnom registru pomoću dvojnog komplementa.

Zadatak 2:

U registru duljine 8 bitova zapisan je sadržaj 10011101. Koji je to dekadski broj, ako znamo da je zapisan pomoću dvojnog komplementa?

3.1. Zadatci s provedenih ispita

  1. (2010, ljetni rok, zadatak 15) Koji se najmanji cijeli broj (u dekadskome brojevnome sustavu) može zapisati u 8-bitovnom registru ako se za zapis cijeloga broja rabi metoda dvojnoga komplementa?
    A. −256
    B. −255
    C. −128
    D. −127

  2. (2010, jesenski rok, zadatak 15) Koji se najveći cijeli broj (u dekadskome brojevnome sustavu) može zapisati u 8-bitovnome registru ako se za zapis cijeloga broja rabi metoda dvojnoga komplementa?
    A. 127
    B. 128
    C. 255
    D. 256

  3. (2011, ljetni rok, zadatak 12) U 8-bitovnome registru zapisan je sljedeći sadržaj: 01010101.
    O kojem se dekadskome broju radi ako je poznato da je to zapis cijeloga broja metodom dvojnoga komplementa?
    A. –171
    B. –43
    C. 85
    D. 171

  4. (2011, jesenski rok, zadatak 12) U 8-bitovnome registru zapisan je sljedeći sadržaj: 00110011.
    O kojem se dekadskome broju radi ako je poznato da je to zapis cijeloga broja metodom dvojnoga komplementa?
    A. –205
    B. –51
    C. 51
    D. 205

  5. (2012, ljetni rok, zadatak 11) Za prikaz brojeva koristi se registar duljine 1 B i metoda dvojnog komplementa.
    Koji će biti prikaz broja –35?
    A. 00100011
    B. 00100100
    C. 11011101
    D. 11011100

  6. (2012, ljetni rok, zadatak 12) Pretpostavimo da se cijeli brojevi u memoriji računala zapisuju u 8-bitovnim registrima metodom dvojnog komplementa. U dvama registrima zapisane su dekadske vrijednosti –73(10) i –83(10). U treći registar treba spremiti zbroj sadržaja ovih registara.
    Koji je sadržaj trećeg registra?
    A. 01100100
    B. 10011100
    C. 000001010
    D. 101100100

  7. (2012, ljetni rok, zadatak 27) Osobe A, B i C igraju jednu zanimljivu igru. Osoba A kaže osobi B jedan cijeli broj. Osoba B treba taj broj zapisati na način kako bi bio zapisan u 8-bitovnom registru metodom dvojnog komplementa. Tako dobiveni zapis osoba B kaže osobi C, ali joj kaže da je to zapis cijelog broja metodom predznaka i apsolutne vrijednosti te osoba C treba naći pripadnu dekadsku vrijednost tog broja.
    Koji bi broj trebala dobiti osoba C ako je osoba A rekla osobi B broj –57?

  8. (2012, jesenski rok, zadatak 12) Pretpostavimo da se cijeli brojevi u memoriji računala zapisuju u 8-bitovnim registrima metodom dvojnog komplementa. U dvama registrima zapisane su dekadske vrijednosti 93(10) i 49(10). U treći registar treba spremiti zbroj sadržaja ovih registara.
    Koji je sadržaj trećeg registra?
    A. 142(10)
    B. –142(10)
    C. –114(10)
    D. 114(10)

  9. (2012, jesenski rok, zadatak 27) Osobe A, B i C igraju jednu zanimljivu igru. Osoba A kaže osobi B jedan cijeli broj. Osoba B treba taj broj zapisati na način kako bi bio zapisan u 8-bitovnom registru metodom predznaka i apsolutne vrijednosti. Tako dobiveni zapis osoba B kaže osobi C, ali joj kaže da je to zapis cijelog broja metodom dvojnog komplementa te osoba C treba naći pripadnu dekadsku vrijednost tog broja.
    Koji bi broj trebala dobiti osoba C ako je osoba A rekla osobi B broj –37?

  10. (2013, ljetni rok, zadatak 27) Iva, Luka i Marko igraju zanimljivu igru. Iva kaže Luki jedan cijeli broj. Luka treba taj broj zapisati na način kako bi bio zapisan u 8-bitovnome registru metodom predznaka i apsolutne vrijednosti. Tako dobiveni zapis Luka kaže Marku, ali mu kaže da je to zapis cijeloga broja metodom dvojnoga komplementa. Marko treba naći pripadnu dekadsku vrijednost toga broja.
    Koji bi broj trebao dobiti Marko ako je Iva rekla Luki broj –5?

  11. (2013, jesenski rok, zadatak 11) Sadržaj 8-bitovnoga registra je 10001001. O kojem se dekadskome broju radi ako se zna da je u registru zapisan cijeli broj metodom dvojnoga komplementa?
    A. -119
    B. -9
    C. 119
    D. 137

  12. (2013, jesenski rok, zadatak 12) U 8-bitovnim registrima zapisuju se cijeli brojevi metodom dvojnoga komplementa.
    Na slici su prikazani sadržaji registara A i B.
    Koji će biti dekadski ekvivalent sadržaja 8-bitovnoga registra C ako je u njemu zapisan zbroj sadržaja registara A i B?
    sadržaj registara
    A. -51
    B. 49
    C. 207
    D. 305

  13. (2013, jesenski rok, zadatak 27) Lovro, Nina i Josip igraju zanimljivu igru. Lovro kaže Nini jedan cijeli broj. Nina treba taj broj zapisati na način kako bi bio zapisan u 8-bitovnome registru metodom dvojnoga komplementa. Tako dobiveni zapis Nina kaže Josipu, ali mu kaže da je to zapis cijeloga broja metodom predznaka i apsolutne vrijednosti. Josip treba naći
    pripadnu dekadsku vrijednost toga broja.
    Koji bi broj trebao dobiti Josip ako je Lovro rekao Nini broj -63?

  14. (2014, ljetni rok, zadatak 12) Pretpostavimo da se cijeli brojevi u memoriji računala zapisuju u 8-bitovnim registrima metodom dvojnoga komplementa. U dvama registrima zapisane su dekadske vrijednosti 109 i 53. U treći registar treba spremiti zbroj sadržaja tih dvaju registara.
    Koja je dekadska vrijednost trećega registra ako znamo da se radi o zapisu broja metodom dvojnoga komplementa?
    A. –162
    B. –94
    C. 94
    D. 162

  15. (2014, jesenski rok, zadatak 12) Pretpostavimo da se cijeli brojevi u memoriji računala zapisuju u 8-bitovnim registrima metodom dvojnoga komplementa. U dvama registrima zapisane su dekadske vrijednosti –35 i 14. U treći registar treba spremiti zbroj sadržaja tih dvaju registara.
    Koji je sadržaj trećega registra prikazan u heksadekadskome brojevnom sustavu?
    A. 4F
    B. B1
    C. EB
    D. CF

  16. (2015, ljetni rok, zadatak 12) Na slici su prikazani sadržaji 8-bitovnih registara A i B u kojima su brojevi zapisani metodom dvojnoga komplementa. Koji će biti sadržaj 8-bitovnoga registra C ako je u njemu zapisan zbroj sadržaja registara A i B?
    sadržaj registara
    A. 01110100
    B. 10001000
    C. 110001000
    D. 111101000

  17. (2015, ljetni rok, zadatak 27) Eva, Filip i Lucija igraju zanimljivu igru. Eva kaže Filipu jedan cijeli broj. Filip treba taj broj zapisati na način kako bi bio zapisan u 8-bitovnome registru metodom dvojnoga komplementa. Tako dobiveni zapis Filip kaže Luciji, ali joj kaže da je to zapis cijeloga broja metodom predznaka i apsolutne vrijednosti. Lucija treba naći pripadnu dekadsku vrijednost toga broja.
    Ako je Eva rekla Filipu broj –16, koji bi broj trebala dobiti Lucija?

  18. (2015, jesenski rok, zadatak 11) Za prikaz brojeva u računalu upotrebljava se 8-bitovni registar i metoda dvojnoga komplementa. Koji će biti prikaz broja –6?
    A. 11111010
    B. 10000110
    C. 11111001
    D. 11100000
     
  19. (2015, jesenski rok, zadatak 27) Ivan, Ana i Maja igraju zanimljivu igru. Ivan kaže Ani jedan cijeli broj. Ana treba taj broj zapisati na način kako bi bio zapisan u 8-bitovnome registru metodom predznaka i apsolutne vrijednosti. Tako dobiveni zapis Ana kaže Maji, ali joj kaže da je to zapis cijeloga broja metodom dvojnoga komplementa. Maja treba naći pripadnu
    dekadsku vrijednost tog broja.
    Ako je Ivan rekao Ani broj –22, koji bi broj trebala dobiti Maja?

  20. (2015, jesenski rok, zadatak 28) Koji se najmanji cijeli broj (u dekadskome brojevnom sustavu) može zapisati u 8-bitovnome registru ako se za zapis cijeloga broja upotrebljava metoda dvojnoga komplementa?

3.2. Rješenja

  1. C
  2. A
  3. C
  4. C
  5. C
  6. A
  7. -71
  8. C
  9. -91
  10. -123
  11. A
  12. B
  13. -65
  14. B
  15. C
  16. B
  17. -112
  18. A
  19. -106
  20. -128

4. Prikaz relalnih brojeva

Realni brojevi sastoje se od dva dijela odvojena točkom - cjelobrojnog (ispred decimalne točke) i decimalnog (iza decimalne točke).

U svakodnevnom životu realne brojeve zapisujemo u obliku kojeg nazivamo zapis brojeva s fiksnom točkom. Tako su zapisani npr. brojevi 312.422, 14.56, 36532718.31. Takav zapis nije prikladan za zapisivanje jako velikih ili jako malih brojeva, pa se oni zapisuju u tzv. eksponencijalnom zapisu (npr. 3.12422*102).

Broj zapisan u eksponencijalnom obliku sastoji se od normalizirane mantise (ispred decimalne točke nalazi se samo jedna znamenka) i eksponenta.

U prethodnom primjeru normalizirana mantisa je 3.12422, a eksponent je 2.

Na sličan način zapisuju se realni brojevi i u računalu. Danas se koristi nekoliko standarda, a jedan od njih je IEEE 754 standard (ili norma).

Kako zapisujemo broj prema IEEE 754 notaciji?

  • Odredimo predznak - 0 za pozitivne, a 1 za negativne brojeve
  • Realan broj najprije pretvorimo u binarni (npr. 12.5 = 1100.1(2)).
  • Dobiveni binarni broj zapišemo u eksponencijalnom obliku. Pošto se ispred decimalne točke može nalaziti samo jedinica, ona se u računalu ne pohranjuje i naziva se skrivenim bitom (1.1001*23 => mantisa je 1001, a 3 je binarni eksponent - binarni jer je baza 2)
  • Binarni eksponent uvećamo za 127 (da izbjegnemo prikaz negativnog eksponenta) i tako dobiveni broj pretvorimo u binarni (3+127=130=10000010(2)).
  • Popunimo 32 bita po sljedećem principu: Prvi bit je predznak (0 ili 1), sljedećih osam bitova popunimo sa binarnim eksponentom uvećanim za 127, a ostalih 23 bita popunimo s mantisom (dio iza decimalne točke). Ako mantisa sadrži manje od 23 bita dopunimo je s nulama (01000001010010000000000000000000).

Brojeve u IEEE 754 standardu često zbog kraćeg zapisa prikazujemo u heksadekadskom brojevnom sustavu.

Prikaz broja prema IEEE standardu u heksadekadskom brojevnom sustavu na primjeru dekadskog broja 5.25. pogledajte ovdje.

Zadatak 1:

Prikaži realan broj 9.6875(10) u heksadekadskom obliku prema IEEE 754 standardu jednostruke preciznosti! 

Primjer:

Koja je vrijednost prikazana u 32-bitnom registru postavljenom na standardnu točnost?
10111101010000000000000000000000(2)

Predznak je 1 => broj je negativan

Binarni eksponent uvećan za 127 = 01111010(2) = 122

Binarni eksponent = 122 - 127 = -5

Mantisa: 1.1 => traženi broj je -1.1*2-5 = -0.000011(2) = -0.046875

Zadatak 2:

Koje su vrijednosti prikazane u 32-bitnom registru, postavljenom na standardnu točnost?

  • C1F00000(16)

  • 3A800000(16)

  • 41910000(16)

4.1. Zadatci s provedenih ispita

  1. (2012, ljetni rok, zadatak 28) Realni broj –125,125 prikazan je u računalu prema IEEE 754 standardu jednostruke preciznosti.
    Koja je heksadekadska vrijednost tog zapisa?

  2. (2012, jesenski rok, zadatak 28) Zadan je heksadekadski zapis sadržaja četiriju uzastopnih bajtova koji predstavljaju zapis realnog broja prema IEEE 754 standardu jednostruke preciznosti. Zapis ima sljedeći oblik: C2120000.
    O kojem se broju u dekadskom brojevnom sustavu radi?

  3. (2013, ljetni rok, zadatak 12) U 32-bitovnome registru zapisan je broj prema IEEE 754 standardu. Heksadekadski ekvivalent zapisa broja je C13E0000.
    Koji će dekadski broj biti prikazan na zaslonu monitora?
    A. –11,875
    B. –3,875
    C. 3,875
    D. 11,875

  4. (2013, jesenski rok, zadatak 28) Prikažite realan broj 5,375(10) u heksadekadskome obliku prema IEEE 754 standardu jednostruke preciznosti.

  5. (2014, ljetni rok, zadatak 28)  Zadan je heksadekadski zapis sadržaja četiriju uzastopnih bajtova koji predstavljaju zapis realnoga broja prema IEEE 754 standardu jednostruke preciznosti. Zapis ima sljedeći oblik: 432C8000.
    Koji je to broj u dekadskome brojevnom sustavu?

  6. (2014, jesenski rok, zadatak 28)  Zadan je heksadekadski zapis sadržaja četiriju uzastopnih bajtova koji predstavljaju zapis realnoga broja prema IEEE 754 standardu jednostruke preciznosti. Zapis ima sljedeći oblik: BE000000.
    Koji je to broj u dekadskome brojevnom sustavu?

  7. (2015, ljetni rok, zadatak 28)  Pretpostavimo da se realni brojevi u memoriji računala zapisuju prema IEEE 754 standardu. Ako je u registru zapisan broj čija je heksadekadska vrijednost C0480000, koji je to dekadski broj?

  8. (2015, jesenski rok, zadatak 12)  Realan broj –7,125 prikazan je u računalu prema IEEE 754 standardu jednostruke preciznosti. Koja je heksadekadska vrijednost toga zapisa?
    A. 40E40000
    B. C0E40000
    C. C0F00000
    D. 40F00000

  9. (2016., ljetni rok, zadatak 28) IEEE 754 standard jednostruke preciznosti, kojim se računalo koristi za zapis realnoga broja, sastoji se od predznaka, karakteristike i mantise. Koliko je bitova ostavljeno za mantisu u tome zapisu?

4.2. Rješenja

  1. C2FA4000
  2. -36.5
  3. A
  4. 40AC0000
  5. 172.5
  6. -0,125
  7. -3.125
  8. B
  9. 23

5. Prikaz slova i ostalih znakova

Za prikaz znakova i slova koriste se dogovoreni načini zapisivanja. Svako se slovo ili znak zapisuje pomoću jedinstvene kombinacije nula i jedinica - koda.

Da bi se sva računala međusobno "razumjela", potrebno je uvesti standard u zapis znakova. Postoji nekoliko standardnih kodova. Jedan od najpoznatijih je ASCII kod. ACCII kod temeljen je na engleskoj abecedi i svaki znak prikazuje se pomoću 7 bitova. Danas se koristi prošireni, 8-bitni, ASCII kod kojim se može prikazati 256 različitih znakova. Na taj način omogućilo se zapisivanje slova specifičnih za neke europske zemlje (tako i slova č, ć, ž, š i đ).

Za prikaz hrvatskih slova danas se koriste dva standarda Central European (Windows 1250) i  Central European (ISO 8852).

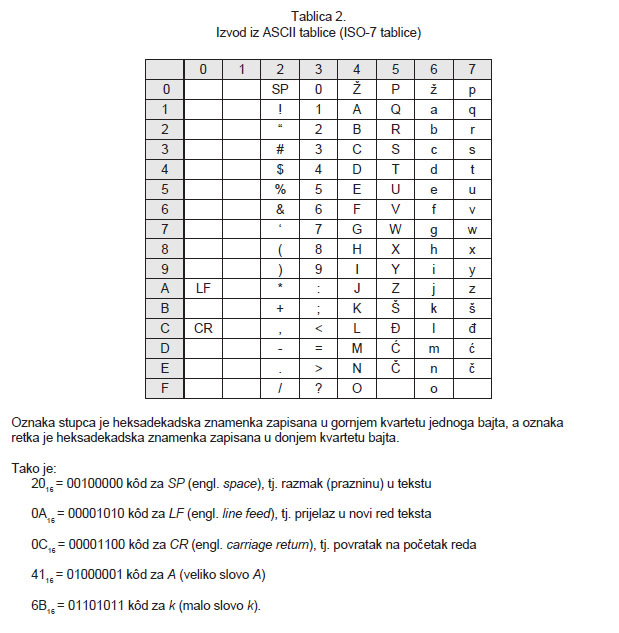
Izvod iz ASCII tablice dan je u prvom poglavlju "Potrebni dokumenti i informacije o Državnoj maturi iz informatike".

Niti prošireni ASCII kod nije dovoljan za prikaz svih znakova svih svjetskih jezika.  Zbog toga se danas koristi još jedan način zapisivanja - UNICODE. Svaki se znak u UNICODE kodu zapisuje pomoću 16 binarnih znamenki.

Prvih 128 znakova proširenog ASCII koda i UNICODE su identični znakovima standardnog ASCII koda.

Zadatak 1

Koliko različitih znakova se može zapisati standardnim ASCII kodom, koliko proširenim, a koliko UNICODE kodom?

Primjer

U 8-bitnom registru zapisan je sadržaj 00110011. O kojem se sadržaju radi ako znamo da je znak zapisan proširenim ASCII kodom?

Binarni broj 00110011 zapisan u dekadskom brojevnom sustavu je 51. Ako pogledamo u tablicu, vidjet ćemo da je na 51. mjestu zapisan broj 3.

Zadatak 2

U 8-bitnom registru zapisan je sadržaj 11010011. O kojem se sadržaju radi ako znamo da je znak zapisan proširenim ASCII kodom?

Zadatak 3

U nizu 8-bitnih registara zapisan je sadržaj:
01101101
01100001
01110100
01110101
01110010
01100001

O kojem se sadržaju radi ako znamo da su znakovi zapisani proširenim ASCII kodom?

Zadatak 4

Znak + zapišite u 8-bitnom registru proširenim ASCII kodom.

5.1. Zadatci s provedenih ispita

  1. (2010, ljetni rok, zadatak 16) Niz heksadekadskih vrijednosti 53 54 49 4C predstavlja tekst zapisan ASCII kodom.
    Koji je tekst zapisan tim nizom (rabite tablicu 2.)?
    A. STOL
    B. BROJ
    C. KRAJ
    D. STIL
    tablica2

  2. (2010, ljetni rok, zadatak 29) Koliko će prostora (u megabajtima) u memoriji zauzeti datoteka u kojoj je  pohranjano 128 stranica teksta ako na jednu stranicu pisanu u tekstualnome editoru stane 4096 znakova, a za zapis znaka rabimo 16-bitovni kôd?

  3. (2010, jesenski rok, zadatak 16) Koji tekst predstavlja niz heksadekadskih vrijednosti 53 54 4F 4C zapisan ASCII kôdom (rabite tablicu 2.)?
    A. STIL
    B. BROJ
    C. KRAJ
    D. STOL

  4. (2011, ljetni rok, zadatak 16) Na pisaču se ispisuje tekst zapisan ASCII kodom predstavljen nizom heksadekadskih vrijednosti: 4D 61 20 6D 61.
    Kako će izgledati ispis (rabite tablicu 2.)?
    A. Ma
        ma
    B. MA
        MA
    C. MA MA
    D. Ma ma

  5. (2011, ljetni rok, zadatak 29) Pohranjeni tekst na tvrdome disku zauzima 700 KB.
    Koliko stranica ima taj tekst ako se na jednoj stranici nalazi 1600 znakova kodiranih UNICODE-16 kodom?

  6. (2011, jesenski rok, zadatak 16) Na pisaču se ispisuje tekst zapisan ASCII kodom predstavljen nizom heksadekadskih vrijednosti: 4D 20 61 6D 61.
    Kako će izgledati ispis (rabite tablicu 2.)?
    A. M ama
    B. M
        AMA
    C. M AMA
    D. M
        ama

  7. (2012, ljetni rok, zadatak 26) Koliko će prostora u kilobajtima na tvrdom disku zauzeti 512 stranica čistog teksta ako je poznato da se na jednoj stranici teksta nalazi 800 znakova, a za kodiranje znakova koristi se UNICODE 16 kôd?

  8. (2012, jesenski rok, zadatak 26) Pohranjeni tekst na tvrdom disku zauzima 600 KB. Koliko stranica ima taj tekst ako se na jednoj stranici nalazi 800 znakova kodiranih UNICODE 16 kôdom?

  9. (2013, jesenski rok, zadatak 26) Koliko će prostora (u kilobajtima) na tvrdome disku zauzeti 512 stranica čistoga teksta ako je poznato da se na jednoj stranici teksta nalazi 2 800 znakova, a za kodiranje znakova upotrebljava se prošireni ASCII kôd?

  10. (2014, ljetni rok, zadatak 11) Koliko se različitih znakova može kodirati s pomoću proširenoga ASCII kôda?
    A. 7
    B. 8
    C. 128
    D. 256

  11. (2014, ljetni rok, zadatak 26) Koliko će prostora u kilobajtima zauzeti tri stranice teksta ako se na svakoj stranici nalaze 1024 znaka, a znakovi su kodirani proširenim ASCII kôdom?

  12. (2014, ljetni rok, zadatak 27) U 8-bitovnome registru zapisano je slovo T koje je kodirano proširenim ASCII kôdom.
    Koji bi to cijeli broj bio ako bismo na sadržaj registra gledali kao na zapis cijeloga broja s predznakom i apsolutnom vrijednosti?

  13. (2014, jesenski rok, zadatak 11) Koliko će bitova imati riječ „matura” ako je kodiramo proširenim ASCII kôdom?
    A. 6
    B. 42
    C. 48
    D. 96

  14. (2015, jesenski rok, zadatak 26) Koliko će prostora (u KB) na tvrdome disku zauzeti 256 stranica čistoga teksta ako je poznato da se na jednoj stranici teksta nalazi 3000 znakova, a za kodiranje znakova upotrebljava se prošireni ASCII kôd?
    (Napomena: 1 KB = 210 B)

  15. (2016., ljetni rok, zadatak 11) Ako neki podatak može poprimiti jednu od 64 različite vrijednosti, koliko je minimalno bitova potrebno za zapis toga podatka?
    A. 6
    B. 8
    C. 64
    D. 512

  16. (2016., ljetni rok, zadatak 26)  Koliko će prostora u kilobajtima zauzeti deset stranica teksta ako se na svakoj stranici nalazi 512 znakova, a znakovi su kodirani proširenim ASCII kodom?

5.2. Rješenja

  1. D
  2. 1 MB
  3. D
  4. D
  5. 224
  6. A
  7. 800 KB
  8. 384
  9. 1400 KB
  10. D
  11. 3
  12. 84
  13. C
  14. 750 KB
  15. A
  16. 5

5.3. Izvod iz ASCII tablice

ASCII

Detaljniji opis znakova u ASCII tablici pogledajte ovdje.