Kružnica u koordinatnom sustavu
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | Kružnica u koordinatnom sustavu |
| Knjiga: | Kružnica u koordinatnom sustavu |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | četvrtak, 3. travnja 2025., 10:29 |
Opis
Kružnica je svuda oko nas. Ona budi ljudski interes oduvijek. Mnogi čuveni matematički zadaci vezani su uz kružnicu i krug. Što je kružnica? Kružnica je skup točaka T ravnine koje su jednako udaljene od jedne čvrste točke – središta S Udaljenost točke T od središta S zove se polumjer ili radijus kružnice. Definiciju kružnice možemo zapisati u obliku jednakosti |ST|=r. Primjer 1. Odredimo skup svih točaka ravnine čije udaljenosti od točke S(2, -2) iznose 3 jedinice. Neka je T(x, y) bilo koja od traženih točaka. Njezina udaljenost od točke S(2, -2) mora biti 3. Prisjetimo se formule za izračunavanje udaljenosti točaka u koordinatnom sustavu. |TS|= $$ \sqrt{\left(x-2\right)^{2} +\left(y+2\right)^{2}}=3$$ Kvadrirajmo gornju jednadžbu: (x-2)2 + (y+2)2 = 9 Ova jednadžba predstavlja jednadžbu kružnice čije je središte u točki S(2, -2), a polumjer joj je 3. 
kružnice.
Jednadžba kružnice
Kružnica je svuda oko nas. Ona budi ljudski interes oduvijek. Mnogi čuveni matematički zadaci vezani su uz kružnicu i krug.
Što je kružnica? 
Kružnica je skup točaka T ravnine koje su jednako udaljene od jedne čvrste točke – središta S kružnice. Udaljenost točke T od središta S zove se polumjer ili radijus kružnice.
Definiciju kružnice možemo zapisati u obliku jednakosti |ST|=r.
Primjer 1.
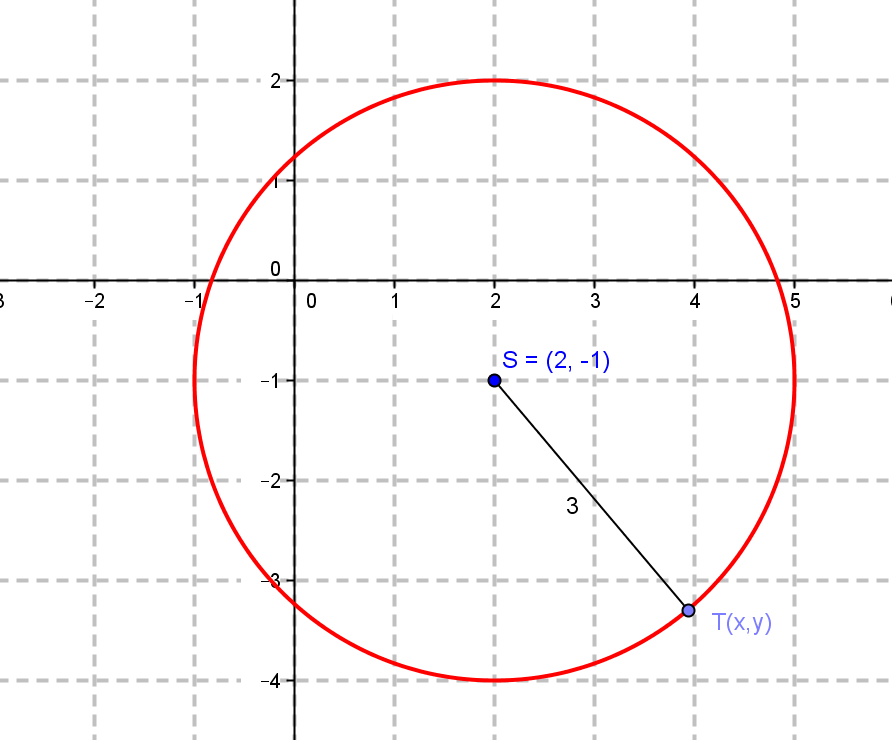
Odredimo skup svih točaka ravnine čije udaljenosti od točke S(2, -2) iznose 3 jedinice.
|
Neka je T(x, y) bilo koja od traženih točaka. Njezina udaljenost od točke S(2, -2) mora biti 3. Prisjetimo se formule za izračunavanje udaljenosti točaka u koordinatnom sustavu.
Kvadrirajmo gornju jednadžbu: (x-2)2 + (y+2)2 = 9 Ova jednadžba predstavlja jednadžbu kružnice čije je središte u točki S(2, -2), a polumjer joj je 3.
|
