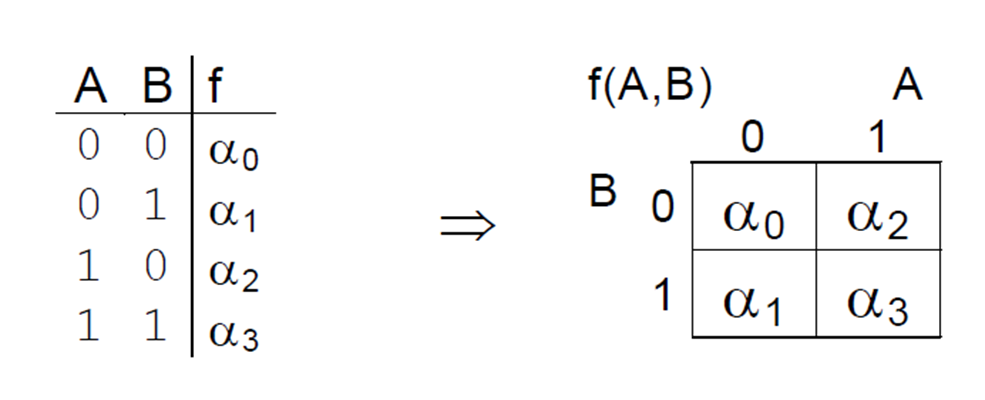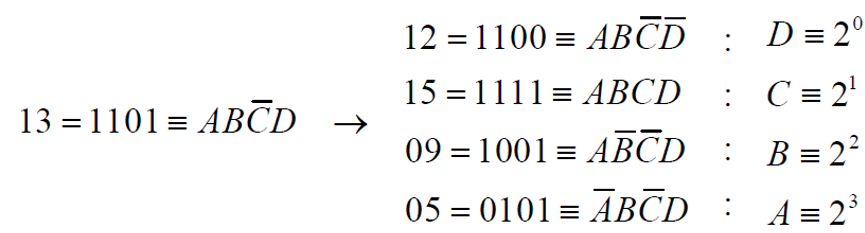Boolova algebra
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | Digitalna logika |
| Knjiga: | Boolova algebra |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | subota, 23. studenoga 2024., 05:04 |
1. Boolova Algebra
Pravila za množenje i zbrajanja
Askiomi i teoremi boolove algebre
K tablice
1.1. Pravila za množenje
1. Svaki broj pomnožen s 0 daje 0
2. Svaki broj pomnožen s 1 daje taj isti broj
3. Svaki broj pomnožen sam sa sobom daje taj isti broj
4. Svaki broj pomnožen sa svojom negacijom daje 0
1.2. Pravila za zbrajanje
1. Svaki broj zbrojen s 1 daje 1
2. Svaki broj zbrojen s 0 daje taj isti broj
3. Svaki broj zbrojen sam sa sobom daje taj isti broj
4. Svaki broj zbrojen sa svojom negacijom daje 1
1.3. Zakon komutacije
Zakoni komutacije pokazuju da redoslijed dovođenja promjenljive ulazne veličine na ulaze logičkog sklopa nema utjecaja na rezultat logičke operacije.
\( A+B=B+A \)
\( A \cdot B= B \cdot A \)
1.4. Zakon distribucije
Zakoni distribucije pokazuju da grupacija pojedinih članova (zbrajanja ili množenja) sklopa nema utjecaja na rezultat logičke operacije.
\( A \cdot B \cdot C = (A \cdot B) \cdot C =A \cdot (B \cdot C) =B \cdot (A \cdot C) \)
\( A + B + C = (A+ B) + C =A + (B + C) =B + (A + C) \)
1.5. Zakon asocijacije
Zakoni asocijacije pokazuju da redoslijed operacija koje se vrše nad pojedinim članovima nema utjecaja na rezultat logičke operacije.
\( A \cdot(B+C)=A \cdot B+A \cdot C \)
\( A+(B \cdot C) =(A+B) \cdot (A+C) \)
1.6. De Morganovi teoremi
De Morganovi teoremi prikazuju promjenu koju je moguće napraviti nad operacijom ukoliko je operator pod negacijom. Ukoliko je zbrajanje pod negacijom ono postaje množenje i obratno.
\( \overline{A \cdot B} = \overline{A} + \overline {B} \)
\( \overline{A + B} = \overline{A} \cdot \overline {B} \)
1.7. Video Aksiomi i osnovni teoremi Boolove algebre
1.8. K tablice
Booleova algebra predstavlja bazu za pojednostavljenje logičkih krugova. Jedna od metoda pojednostavljenja Boole-ovih funkcija koristi Karnaughove tablice. Metoda se ubraja u grafičke metode.
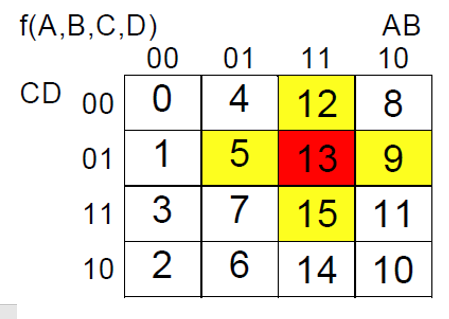
minimizacija ~ "grupiranje" polja: temeljeno na ljudskoj sposobnosti raspoznavanja uzoraka (1 i 0)
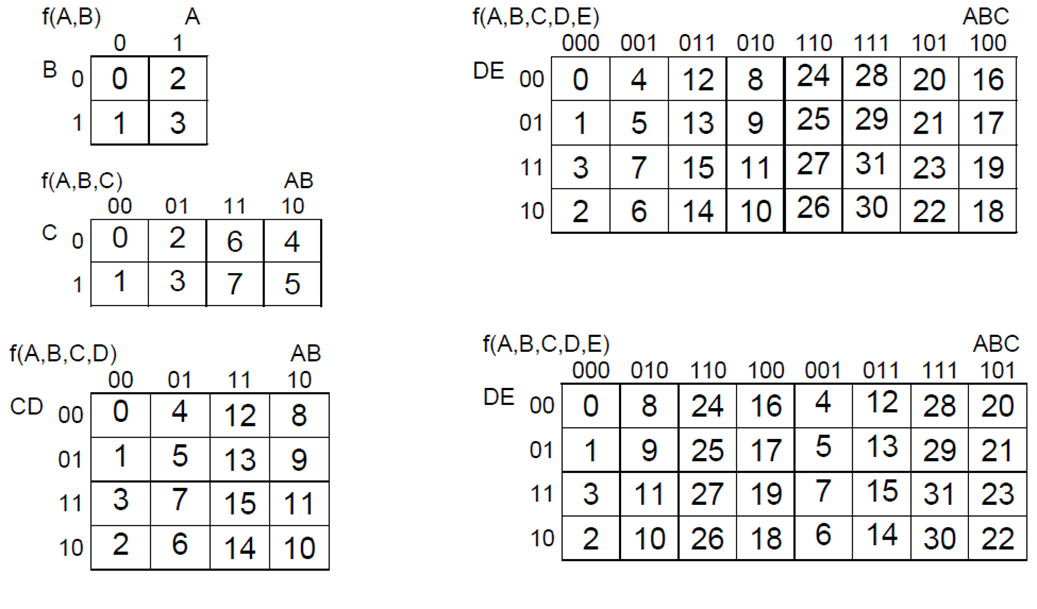
• K-tablice za n > 2 varijable ~ simetrija oko jedne stranice, superpozicija
• praktična primjena: n ≤ 6
