Otisni knjiguOtisni knjigu

Pretvorbe brojeva iz jednog brojevnog sustava u drugi

Sjedište: CARNET - Arhiva 2021 Loomen
E-kolegij: Informatika 1 - Gimnazija Đakovo
Knjiga: Pretvorbe brojeva iz jednog brojevnog sustava u drugi
Otisnuo/la: Gost (anonimni korisnik)
Datum: četvrtak, 19. prosinca 2024., 07:58

Opis

Kako saznati vrijednost binarnog, oktalnog ili heksadekadskog broja?

Sadržaj

1. Uvod

uvodna

Naučili smo da se u radu s računalom koriste binarni, oktalni i heksadekadski brojevni sustav.

Znači, računalo te brojeve prepoznaje. Ali kako ćemo mi znati vrijednost brojeva zapisanih u tim sustavima? Možemo li zadani binarni broj prikazati u oktalnom ili heksadekadskom brojevnom sustavu? A obrnuto?

2. Pretvorba binarnog i heksadekadskoga broja u dekadski i obrnuto

sustavi

Pretvorba broja zapisanog u nekoj bazi u dekadski broj odvija se preko težinskih vrijednosti znamenaka. Svaka se znamenka pomnoži s potencijama baze, idući s desna na lijevo. Krajnja desna potencija je nula.

Pretvorba dekadskoga broja u broj u nekoj drugoj bazi odvija se prema sljedećem pravilu:

  • Dekadski broj dijeli se s bazom.
  • Postupak se ponavlja sa svakim kvocijentom sve dok se ne dobije kvocijent 0.
  • Prilikom svakog dijeljenja nastaju ostatci (od 0 do b-1, gdje je b baza).

Zapisivanjem ostataka od posljednjega prema prvome dobije se zapis dekadskoga broja u traženoj bazi.

 

2.1. Tablica potencija brojeva 2 i 16

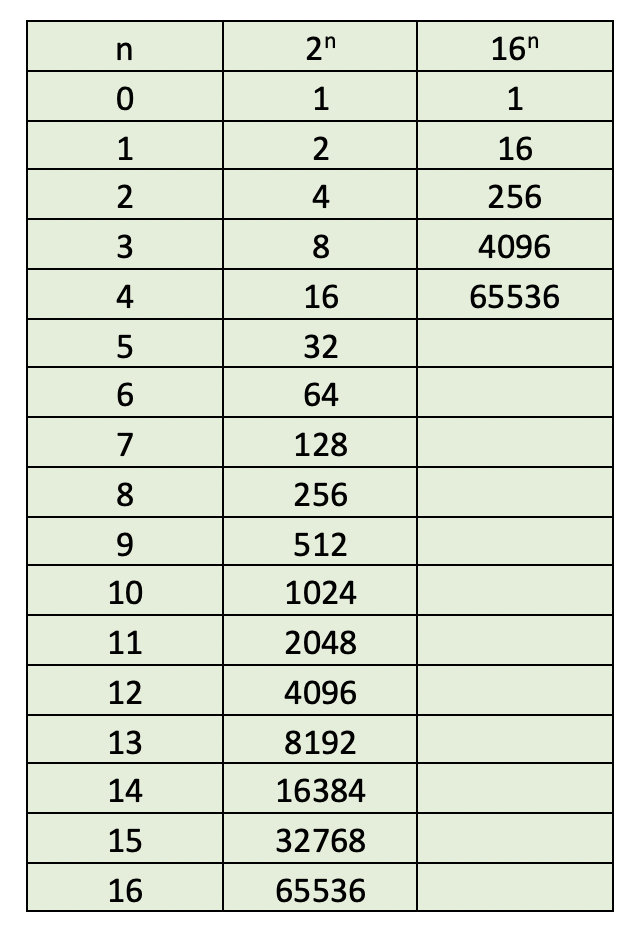
tablice potencija

2.2. Brži način pretvorbe binarnog broja u dekadski i obrnuto

Pretvorba binarnoga broja u dekadski

Za bržu pretvorbu binarnoga broja u dekadski možemo iskoristiti činjenicu da je binarni brojevni sustav pozicijski što znači da vrijednost znamenke ovisi o njezinom mjestu u broju.

Iznad svake znamenke (krenuvši od krajnje desne) zapišimo njezinu težinu (potenciju broja 2). Nakon toga jednostavno zbrojimo sve težine ispod kojih se nalazi znamenka 1.

Pogledajmo na primjeru:

Neka je zadan binarni broj 1011(2). Iznad svake znamenke zapišimo njezinu težinu (baza je broj 2, a eksponent mjesto znamenke).


Jednostavno, zar ne?

Za vježbu pokušajte s binarnim brojevima 101101 i 11110.

Pretvorba dekadskoga broja u binarni

Za ovu pretvorbu možemo iskoristiti jednaku logiku. Potrebno je samo obrnuti postupak.

Kao i u prethodnoj pretvorbi, krenemo s raspisivanjem potencija broja dva. Zapisujemo ih sve dok ne dođemo do potencije koja je veća ili jednaka zadanom dekadskome broju.
Sada pokušamo doći do zadanog broja zbrajanjem težina. Ispod težine koju smo iskoristili zapišemo znamenku 1, a ispod one koju nismo iskoristili zapišemo nulu.

Pogledajmo na primjeru. Neka je zadan dekadski broj 21.
Zapišimo potencije broja 2 i slijedimo upute napisane u prethodnom odlomku:


Za vježbu prikažite dekadske brojeve 31 i 17 u binarnom brojevnom sustavu.

2.3. Vježba

Pokreni i odigraj igru naziva Binary game.

Odaberi jedan od linkova:

https://learningcontent.cisco.com/games/binary/index.html ili

https://studio.code.org/projects/applab/iukLbcDnzqgoxuu810unLw

2.4. Pitanja, vježbe i zadatci

zadatak

  1. Binarne brojeve 101(2), 11001(2) i 11111(2) prikaži u dekadskom brojevnom sustavu.
  2. Heksadekadske brojeve 10(16), 15(16) i 101(16) prikaži u dekadskom brojevnom sustavu.
  3. Dobivena rješenja provjeri programom kalkulator koji se nalazi u skupini programa Pomagala (Accessories)..
  4. Dekadske brojeve 12, 87 i 214 prikaži u binarnom i heksadekadskom brojevnom sustavu.
  5. Popuni tablicu:
    dekadski binarni heksadekadski
    127
    128
    255
    256
    100
    41
    11111

     

  6. Koji je heksadekadski zapis dekadskoga broja 58?
    a) A3 
    b) E2 
    c) 3A 
    d) 2E
     
  7. Poredaj po veličini sljedeće brojeve počevši od najmanjeg: 
    a) 5A(16)   
    c) 92(10) 
    d) 1011011(2)
     
  8. Poredaj po veličini sljedeće brojeve počevši od najmanjeg: 
    a) 43(16) 
    c) 68(10) 
    d) 1000010(2) 

3. Pretvorba heksadekadskoga broja u binarni i obrnuto

  • Heksadekadski broj pretvaramo u binarni tako da svaku heksadekadsku znamenku prikažemo pomoću četiri binarne
  • Binarni broj pretvaramo u heksadekadski tako da, krenuvši s desna na lijevo, odvajamo po četiri binarne znamenke. Svaku skupinu pretvorimo u jednu heksadekadsku znamenku.

3.1. Pitanja, vježbe i zadatci

Pitanja, vježbe i zadatci


1. Opiši postupak pretvaranja heksadekadskog broja u binarni.

2. Zapiši heksadekadske znamenke A, B, C, D, E I F u binarnome brojevnom sustavu.

3. Koji je binarni zapis heksadekadskoga broja BCDE?
    a) 1011110011011110(2) 
    b) 1011110110111110(2) 
    c) 1100101111011110(2) 
    d) 1110110111001011(2)

4. Koji je binarni zapis broja  1234(16)? 

5. Koji je binarni zapis broja 536B(16)?

6. Koji je binarni zapis broja 9E7D(16)?

7. Koliko znamenaka „1” ima broj 920F(16) kada je zapisan u binarnom brojevnome sustavu?

8. Koliko znamenaka „0” ima broj 3887(16) kada je zapisan u binarnom brojevnom sustavu (ako se prilikom zapisivanja ne zapisuje vodeće nule)?

9. Na koji način se binarni broj prikazuje u heksadekadskome brojevnom sustavu?

10. Prikaži broj 1111101011101(2) u šesnaestičnom (heksadecimalnom) sustavu.

11. Prikaži broj 11010111100111(2)u šesnaestičnom (heksadecimalnom) brojevnom sustavu.

4. A što s racionalnim brojevima?

Kada binarni, oktalni ili heksadekadski brojevi u svom zapisu sadrže i decimalnu točku (racionalni brojevi), postupak pretvorbe u dekadski brojevni sustav je jednak kao i kod brojeva bez decimalne točke. 

I tada pretvorbu radimo preko težinskih vrijednosti (mjesta znamenki), s tim da od decimalnog zareza u lijevo mjesta kreću od nule i pozitivna su, dok desno od decimalnog zareza mjesta kreću od minus jedan (-1) i negativna su.

Pretvorba decimalnog dekadskog broja u broj u nekoj drugoj bazi odvija se prema u dva koraka:

  1. Najprije pretvorimo cijeli dio broja (dijeljenjem s bazom i pamćenjem ostataka) 

  2. Zatim pretvorimo decimalni dio broja na sljedeći način:
    1. Decimalni dio broja množimo s bazom i zapisujemo znamenke lijevo od decimalne točke.
    2. Postupak nastavljamo sve dok ne dođemo do željene točnosti

Kod ostalih brojevnih sustava, način pretvorbe iz jednog sustava u drugi je jednak. Jedino je potrebno voditi računa o decimalnoj točki.

4.1. Tablica negativnih potencija

tablica negativnih potencija

4.2. Pitanja, vježbe i zadatci

Pitanja, vježbe i zadatci

  1. Opiši postupak pretvorbe decimalnog dekadskoga broja u binarni i heksadekadski brojevni sustav.

  2. Na koji način se decimalni binarni i heksadekadski brojevi pretvaraju u dekadski brojevni sustav?

  3. Kako heksadekadski broj s decimalnom točkom prikazujemo u binarnome brojevnom sustavu?

  4. Binarne brojeve 101.101(2), 111011.11(2) i 0.111(2) prikaži u dekadskom brojevnom sustavu.  

  5. Heksadekadske brojeve A.BC(16), 101.1(16) i 12.A(16) prikaži u dekadskom brojevnom sustavu.
  6. Što je od navedenoga binarni zapis dekadskoga broja 23.125? 
    a) 11101.001 b) 10111.1111101
    c) 10111.001
    d) 10111.1011111

  7. Koji je od sljedećih brojeva binarni zapis dekadskoga broja 6,75?
    a) 10,1001011
    b) 10,11
    c) 110,1001011
    d) 110,11

  8. Prikažite realni broj 279.625 binarno i heksadecimalno.

  9. Prikažite realni broj 147,75 u binarnom i heksadekadskom sustavu.

  10. Prikaži realni broj 190.3125 binarno.