Opće upute o provođenju ispita
| Sitio: | CARNET - Arhiva 2021 Loomen |
| Curso: | 4.B opća gimnazija, SŠ Marka Marulića Slatina 2020./21, |
| Libro: | Opće upute o provođenju ispita |
| Imprimido por: | Gost (anonimni korisnik) |
| Día: | Thursday, 5 de March de 2026, 19:51 |
1. Upute o provođenju ispita
Matematika je na državnoj maturi obvezni predmet. Pristupnici mogu birati hoće li polagati Matematiku na višoj ili na osnovnoj razini.
Ispitni katalog za državnu maturu iz Matematike temeljni je dokument ispita kojim se jasno opisuje što će se i kako ispitivati na državnoj maturi iz ovoga predmeta na višoj i osnovnoj razini u školskoj godini 2020./2021.
Ispitni katalog sadrži sve potrebne informacije i
detaljna pojašnjenja o obliku i sadržaju ispita. Njime se
jasno određuje što se od pristupnika očekuje na ispitu
na višoj i osnovnoj razini.
U ovoj knjizi nalazi se izdvojeni ključni podatci iz ispitnog kataloga za školsku godinu 2020./2021. Detaljnije možete pročitati na poveznici: https://mk0ncvvot6usx5xu4d.kinstacdn.com/wp-content/uploads/2020/09/MATEMATIKA-2021.pdf
2. Cilj ispita
Cilj je ispita iz Matematike provjeriti u kojoj mjeri pristupnici znaju, tj. mogu:
- upotrebljavati matematički jezik tijekom čitanja, interpretiranja i rješavanja zadataka
- očitavati i interpretirati podatke zadane u analitičkome, tabličnome i grafičkome obliku ili riječima te u navedenim oblicima jasno, logično i precizno prikazivati dobivene rezultate
- matematički modelirati problemsku situaciju, naći rješenje te provjeriti ispravnost dobivenoga rezultata
- prepoznati i upotrebljavati vezu između različitih područja matematike
- upotrebljavati različite matematičke tehnike tijekom rješavanja zadataka
- upotrebljavati džepno računalo
3. Područja ispitivanja
Područja ispitivanja:
- Brojevi i algebra
- Funkcije
- Jednadžbe i nejednadžbe
- Geometrija.
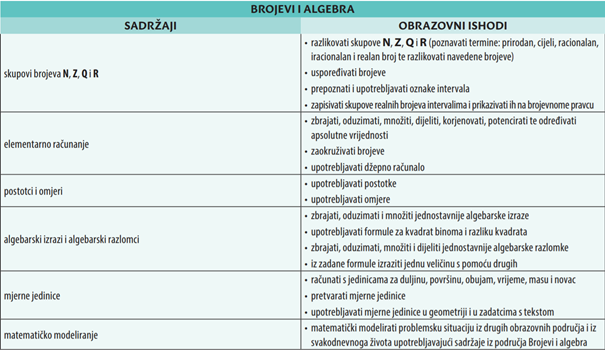
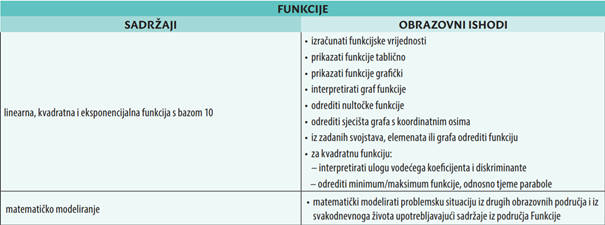
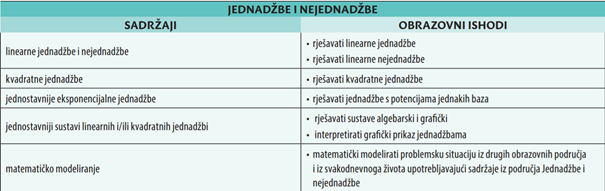
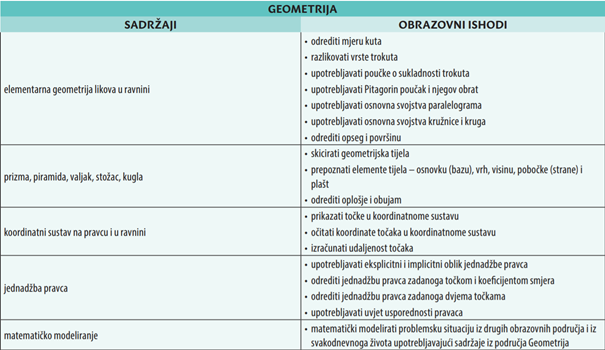
4. Obrazovni ishodi za osnovnu razinu ispita
5. Struktura ispita na osnovnoj razini
U tablici su prikazani udjeli područja ispitivanja na osnovnoj razini ispita:
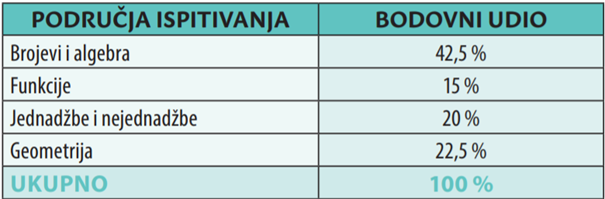
Moguće je odstupanje udjela pojedine cjeline te ono iznosi \( \pm5% \).
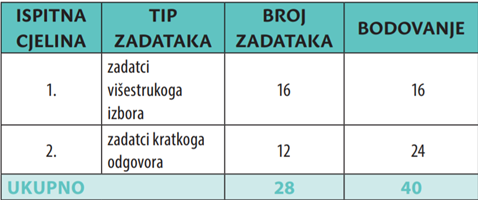
Ispit iz Matematike na osnovnoj razini sadrži 28 zadataka raspoređenih prema tipovima zadataka na sljedeći način:
6. Tehnički opis ispita
-
6.1. Trajanje
Ispit iz Matematike je pisani te se piše bez prekida 150 minuta na osnovnoj razini.
6.2. Izgled ispita
Pristupnik dobiva sigurnosnu vrećicu u kojoj se nalaze:
- Ispitna knjižica
- Knjižica sa formulama* (nalazi se na poveznici https://mk0ncvvot6usx5xu4d.kinstacdn.com/wp-content/uploads/2017/10/MAT-B-formule.pdf)
- List za odgovore
- List za koncept
- Vrećica za povrat
* poželjno je preuzeti formule te ih koristiti prilikom rješavanja zadataka za pripremu kako biste se naviknuli na njih
6.3. Rješavanje ispita
Uz sve vrste zadataka priložena je uputa za rješavanje.
Zadatke višestrukoga izbora pristupnici rješavaju obilježavanjem slova točnoga odgovora između četiriju ponuđenih.
Slova točnih odgovora obilježavaju se znakom X.
Ako u zadatcima višestrukoga izbora pristupnik obilježi više od jednoga odgovora, zadatak će se bodovati s 0 (nula) bodova bez obzira na to što je među obilježenima i točan odgovor.
U zadatcima kratkoga odgovora pristupnici upisuju odgovor na predviđeno mjesto u ispitnoj knjižici.
Za rješavanje zadataka pristupnici mogu upotrebljavati list za koncept, ali moraju, u skladu s navedenim uputama, prepisati ono što se od njih traži na list za odgovore, odnosno u ispitnu knjižicu.
6.4. Pribor
Na ispitu iz Matematike dopušteno je korištenje:
- kemijske olovke (plava ili crna)
- geometrijskog pribora - jedno ravnalo ili jedan trokuta (nije dopuštena upotreba kutomjera i šestara)
- džepno računalo tzv. znanstveni kalkulator (na poveznicama http://dokumenti.ncvvo.hr/Drzavna_matura/2010-03-31/uputa_o_racunalima.pdf i https://mk0ncvvot6usx5xu4d.kinstacdn.com/wp-content/uploads/2019/10/KALKULATORI_20-01-2020.pdf nalaze se opis i popis dopuštenih i zabranjenih džepnih računala)
- knjižica s formulama (dio ispitnog materijala)
Pristupnicima nije dopušteno donijeti niti upotrebljavati nikakve druge listove s formulama.
6.5. Opis bodovanja
Uspješnim rješavanjem ispita na osnovnoj razini pristupnik može ostvariti 40 bodova.
Vrednovanje prve ispitne cjeline (zadataka višestrukoga izbora):
Uspješnim rješavanjem prve ispitne cjeline u ispitu na osnovnoj razini pristupnik može ostvariti 16 bodova.
Ispravno riješen zadatak donosi jedan bod.
Neispravni odgovori ne donose negativne bodove.
Vrednovanje druge ispitne cjeline (zadataka kratkoga odgovora):
Uspješnim rješavanjem druge ispitne cjeline u ispitu na osnovnoj razini pristupnik može ostvariti 24 boda.
Svaki točan odgovor donosi jedan bod.
Svaki ispravno riješen zadatak 16. do 27. u drugoj ispitnoj cjelini (odnosno dio zadatka ako se traži više kratkih odgovora) donosi jedan bod.
Neispravni odgovori ne donose negativne bodove.
U zadatku 28. pristupnik može ostvariti 0, 1 ili 2 boda.
6.6. Česte greške prilikom rješavanja ispita
Česte greške prilikom rješavanja ispita:
- zaokruživanje brojeva:
- Tijekom računanja podatke zadane u zadatku ne treba zaokruživati. Ako su rezultati konačni decimalni brojevi, ne treba ih zaokruživati (osim ako uputom u zadatku nije drugačije navedeno).
- Vrijednosti trigonometrijskih funkcija treba zaokružiti na najmanje četiri decimale.
- Ako se u zadatku traži zaokruživanje na određeni broj decimala, to se odnosi na
konačan rezultat. Međurezultati se tada računaju s točnošću zaokruživanja najmanje na
dvije decimale više od traženog rezultata (primjerice, točnost rezultata na dvije
decimale zahtijeva točnost međurezultata najmanje na četiri decimale).
Broj
π ~ 3.1415926535 8979323 ....
ima beskonačno mnogo decimala pa je prilikom
računanja najbolje koristiti njegovu vrijednost s džepnog računala.
- Neki su brojevi zaokruženi prilikom zadavanja (veliki ili mali brojevi ili brojevi prikazani
u znanstvenom zapisu), stoga su, u zadatcima višestrukog izbora, ponuđena rješenja
zaokružena.
- pojednostavljanje:
- Ako je rezultat racionalan broj zapisan u obliku razlomka, treba ga napisati u obliku do kraja skraćenog razlomka (osim ako uputom u zadatku nije drugačije navedeno).
- Ako je rezultat kompleksan broj, treba ga napisati u standardnom obliku tj. \( a+bi, a,b \in \mathbb{R} \)(osim ako uputom u zadatku nije drugačije navedeno).
- Kod sređivanja algebarskih izraza potrebno je zbrojiti monome istog stupnja,
a algebarske izraze skratiti odgovarajućim faktorima.
- crtanje grafova funkcija:
- Dovoljno je nacrtati dio grafa koji je karakterističan za zadanu funkciju. To najčešće uključuje sjecišta s osima i točke ekstrema (ako postoje). Iz crteža se treba naslutiti domena funkcije, što znači da nije prihvatljiv graf koji završava na nekoj od tih karakterističnih točaka.
- geometrija:
- U formulacijama zadataka pojavljuju se pojmovi skica i slika. Treba ih razlikovati. Skica prikazuje geometrijski objekt čije mjere kutova i duljine dužina ne moraju odgovarati zadanim vrijednostima. Slika je nacrtana u koordinatnom sustavu i svi njeni elementi u skladu su s jediničnim duljinama tog koordinatnog sustava.
Na poveznici https://mk0ncvvot6usx5xu4d.kinstacdn.com/wp-content/uploads/2017/10/MAT-dodatak.pdf nalaze se preporuke za rješavanje ispita upotpunjenje s odgovarajućim primjerima.