Razlaganje programa na manje dijelove - funkcije
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | Informatika 3 PMG - Gimnazija Đakovo |
| Knjiga: | Razlaganje programa na manje dijelove - funkcije |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | petak, 26. prosinca 2025., 03:45 |
Opis
Funkcije u pythonu
Uvodni zadatak
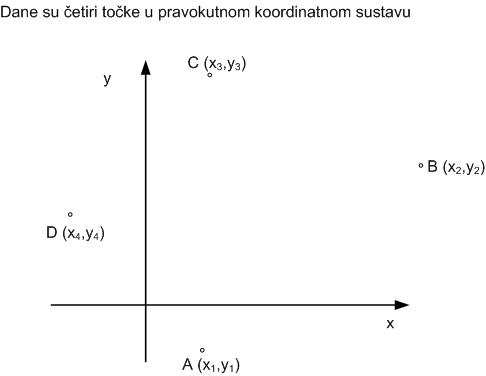
Uvodni zadatak_1
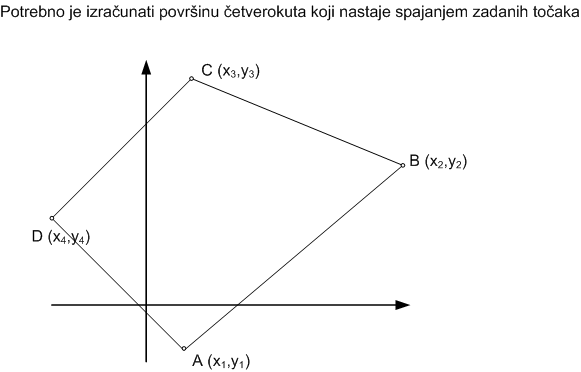
Analiza
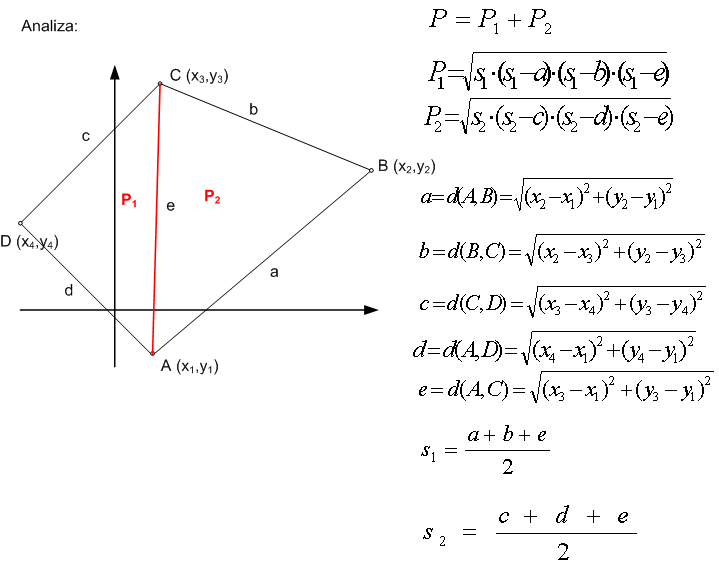
Program
from math import *print('Upiši koordinate točke A(x1,y1)')
x1 = int(input())
y1 = int(input())
print('Upiši koordinate točke B(x2,y2)')
x2 = int(input())
y2 = int(input())
print('Upiši koordinate točke C(x3,y3)')
x3 = int(input())
y3 = int(input())
print('Upiši koordinate točke D(x4,y4)')
x4 = int(input())
y4 = int(input())
a = sqrt(pow(x2-x1,2)+pow(y2-y1,2))
b = sqrt(pow(x3-x2,2)+pow(y3-y2,2))
c = sqrt(pow(x4-x3,2)+pow(y4-y3,2))
d = sqrt(pow(x4-x3,2)+pow(y4-y3,2))
e = sqrt(pow(x1-x3,2)+pow(y1-y3,2))
o1 = a + b + e
s1 = o1/2
p1 = sqrt(s1*(s1-a)*(s1-b)*(s1-e))
o2 = c + d + e
s2 = o2/2
p2 = sqrt(s2*(s2-c)*(s2-d)*(s2-e))
p = p1 + p2
o = a + b + c + d
print('Povrsina zadanog četverokuta je',p,',a opseg',o)
Funkcije
U prethodnom zadatku, za računanje udaljenosti među točkama koristili smo istu formulu, ali sa različitim vrijednostima.Takve dijelove programa praktično je izdvojiti u zasebne cjeline, korisnički definirane funkcije i pozivati ih po potrebi.
Rješavamo li problem na takav način, možemo reći da se bavimo strukturnim programiranjem.
Funkcije u programskom jeziku možemo usporediti sa matematičkim funkcijama. One imaju parametre, a za dane vrijednosti parametara funkcija ima određenu vrijednost. Na primjer, funcija f(x)=x 2, za x=5 ima vrijednost 25.
Možemo reći da funkcije omogućavaju razlaganje problema na jednostavnije i manje cjeline, čime doprinose boljoj preglednost izvornog koda i jednostavnijem pronalaženju i otklanjanju pogrešaka. Također, korištenjem funkcija dolazi do značajnih ušteda memorijskog prostora.
Funkcije se ne moraju koristi samo da bi se izbjeglo višestruko pisanje određenih dijelova programa, već su praktične i ako će se izvršiti samo jednom. U tom slučaju olakšavaju razumijevanje programa, odnosno algoritma.
Definicija funkcije
Ime funkcije iz primjera je kvadrat.
Parametri su vrijednosti koje se iz glavnog programa prenose u funkciju.
U našem primjeru x.
U tijelu funkcije pišemo naredbe .
Obavezan dio tijela funkcije je i naredba return koja rezultat funkcije vraća u glavni program.Primjer definicije funkcije
y = x * x;
return y
Poziv funkcije
Funkcija se izvršava onog trena kad je pozvana iz glavnog programa ili neke druge funkcije.
Za poziv funkcije dovoljno je navesti njeno ime i listu stvarnih argumenata, onim redoslijedom kako su navedeni u najavi funkcije:
ime_funkcije (stvarna lista_argumenata);
Lista argumenata može biti i prazna. Ako je lista prazna onda funkcija koristi globalne varijable.
No obavezno je pisati zagrade (), jer one označavaju da se kontrola tijeka programa prenosi iz nadređene u pozvanu funkciju.
Funkcije se mogu pozivati u izrazima, petljama, ili kao argumenti u pozivima drugih funkcija.
Primjer pozivanja funkcije kvadrat:
- u glavnom programu:
def kvadrat (x):
y = x * x
return y
n = int(input('Upišite jedan cijeli broj: '))
print('Kvadrat broja ',n, 'je ', kvadrat(n))
2. unutar for petlje
def kvadrat (x):
y = x * x
return y
n = int(input('Upišite jedan cijeli broj: '))
for i in range (1, n+1):
print('Kvadrat broja ',i, 'je ', kvadrat(i))
Zadaci za vježbu

- Proučite drugi primjer funkcije u prethodnoj lekciji i odgovorite na pitanje: Što radi ovaj program?
- Riješite uvodni zadatak pomoću funkcije za udaljenost dviju točaka u pravokutnom koordinatnom sustavu (Potrebno je izračunati površinu i opseg četverokuta zadanog s koordinatama svojih vrhova)
- Napravite program za sljedeći problem:
Pretpostavimo da davatelju internet usluga plaćamo račun na sljedeći način: Osnovni paket košta 80 kuna, a svaki dodatni GB još 12 kuna. Izračunajte i ispišite na zaslon koliko će platiti račun korisnik koji je potrošio 2, koliko korisnik koji je potrošio 5, a koliko korisnik koji je potrošio 15 GB. - Preuredite prethodni program tako da ispisuje na zaslon cijene za 1, 2, 3, 4, ... 15 GB prometa.
- Preuredite prethodni program tako da ispisuje koliko treba platiti korisnik koji unese broj potrošenih GB.
- Pomoću funkcije koja traži manji od dva broja pronađi najmanji od tri unesena broja
- Pomoću funkcije koja traži manji od dva broja pronađi najmanji od n unesenih brojeva
- Pomoću funkcije koja ispituje je li jedan broj djeljiv s drugim pronađi sve djelitelje unesenog broja.
- Napravite funkciju koja u glavni program vraća nulu ako je broj prost, a jedinicu ako nije. Koristei funkciju za uneseni broj ispiši na zaslon je li prost ili nije.
Rekurzivne funkcije
Rekurzivna funkcija je funkcija koja poziva samu sebe. U pravilu, rekurzivna rješenja su kraća, ali je za njihovo izvođenje potrebno više vremena i memorije.
Svaka rekurzija mora imati uvjet zaustavljanja koji će omogućiti izlazak iz rekurzije. U protivnom rekurzivna funkcija će se izvoditi beskonačno. Također svaki poziv rekurzije mora se približavati uvjetu zaustavljanja.
Za pohranjivanje rezultata i povratak iz rekurzije upotrebljava se STOG (eng. stack). Stog je dinamički dio memorije koji se upotrebljava za pohranjivanje podataka koji se privremeno koriste u određenim dijelovima programa. Broj podataka na stogu je promjenljiv, ali količina memorije za stog je ograničena.
Stog se puni i prazni prema principu zadnji unutra – prvi van (eng. LIFO – last in – first out). Za bolje razumijevanje stoga često se koristi analogija s hrpom tanjura (npr. u restoranima): posljednji tanjur stavljen na hrpu se uzima prvi.
Na stogu se koriste dvije operacije: push i pop. Operacija push šalje podatak na stog dok operacija pop skida podatak sa stoga.
Primjer rekurzije je izračunavanje n! (n!=1*2*...*n)
Zadatak: Prisjetite se načina na koji smo do sada za zadani broj n računali n!.
Do sada smo koristili definiciju n!=1*2*3*...*n.
No, n! možemo definirati i drugačije: n!=n*(n-1)!.
Ovo je rekurzivni način definiranja n!
Primjeri rekurzivnih funkcija
- Izračunavanje vrijednosti funkcije n! pomoću rekurzije.
Po definiciji je:
0! = 1
1! = 1
2! = 1*2 = 1!*2
3! = 1*2*3 = 2!*3
...
n! = 1*2*3*...*n = (n-1)!*n
Dakle n! se može izračunati ako je poznat (n-1)!, a (n-1)! može se izračunati ako je poznat (n-2)!, itd.
Iz prethodnog razmatranja možemo zaključiti slijedeće: ako računamo umnožak prvih n prirodnih brojeva:
uvjet zaustavljanja je 1!=1,
a opći oblik će biti n!=n*(n-1)! .
Rekurzivna funkcija glasi:
Za nenegativan cijeli broj e slijedeće rekurzivna funkcija računa potenciju be
(uvjet zaustavljanja je za e=0 potencija =1, jer je b0=1, za svaki b>0)
def faktorijel (n):
if n==1:
return 1
else:
return faktorijel(n-1)*n
n = int(input())
print (faktorijel (n)) -
def potencija(b, e):
if e==0:
return 1
else:
return b * potencija(b, e-1)
baza = int(input('Baza: '))
eksponent = int(input('Eksponent: '))
print (potencija (baza, eksponent)) - Fibonaccijev niz je niz brojeva definiran sa:
f(1) = 1
f(2) = 2
f(3) = f(1) + f(2) = 1 + 2 = 3
f(4) = f(2) + f(3) = 2 + 3 = 5
...
f(m) = f(m-2) + f(m-1)
Funkcija:
def fibonacci (n):
if n == 1 or n==2:
return 1
else:
return fibonacci(n-1)+fibonacci(n-2)
n = int(input())
print (fibonacci(n))
Zadaci za vježbu

- Napravite program koji za unesene nenegativne brojeve m i n računa binomni koeficijent $$\binom{n}{m}=\frac{n!\cdot (n-m)!}{m!}$$
- U novoizgrađenoj tvornici prijenosnih računala proizvode se računala sljedećim tempom: prvi mjesec radnici su uspjeli napraviti jedno prijenosno računalo. Sljedeći mjesec napravili su još jedno, a svaki sljedeći mjesec napravili su onoliko računala koliko su ukupno napravili u prethodna dva mjeseca.
Napravite program koji će, rekurzivnom funkcijom, izračunati koliko se u tvornici proizvelo računala nakon n mjeseci (n se unosi).