Teorijski okvir
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | GeoGebra - razvoj modela vođenog učenja otkrivanjem |
| Knjiga: | Teorijski okvir |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | nedjelja, 22. veljače 2026., 22:09 |
Opis
Kratak opis teorijskog okvira i dosadašnjih istraživanja vezanih uz temu
1. Teorija konstruktivizma
Konstruktivizam (engl. constructivist theory) je jedna od kognitivnih teorija učenja koja naglašava nužnost aktivnosti učenika u procesu učenja. Učenik na temelju opažanja i vlastitog iskustva u svojoj fizičkoj i socijalnoj okolini konstruira vlastito znanje koje je stoga jedinstveno za svakog pojedinca. Pri tome je važan aktivan stav osobe koja uči, da bude uključena u ono što se uči, istražuje, postavlja pitanja, stvara hipoteze, rješava probleme i surađuje s drugima.
Konstruktivističkim pristupom učenju mijenja se uloga nastavnika. On više nije primarni izvor informacija već postaje organizator procesa učenja. Njegova uloga je da odabere prikladne oblike rada, nastavne metode, izvore znanja i na taj način oblikuje okolinu za učenje te da potiče i usmjerava učenike u samostalnom otkrivanju novih pojmova, koncepata i zakonitosti.
Konstruktivističko okruženje za učenje matematike dizajnira se tako da učenicima pruža mogućnost za izgradnju konceptualnog razumijevanje te da potiče rješavanje problema i razvija sposobnosti zaključivanja. Pri poučavanju matematike učitelj treba osmisliti odgovarajući model učenikove predodžbe zadane matematičke ideje, a zatim izgraditi provizorni put kojim će se učenici kretati kako bi sami konstruirali tu ideju koja bi bila u suglasju s općeprihvaćenim matematičkim znanjima (Even i Tirosh, 2003).
Jean Piaget, kojega se smatra pionirom konstruktivističke teorije, uvodi pojam genetičke epistemologije - teorije prema kojoj je dijete genetički predodređeno da samostalno konstruira vlastitu spoznaju svijeta oko sebe pod utjecajem socijalnog i kulturnog okruženja. Prema toj teoriji važnu ulogu u procesu učenja ima adaptacija koja se odnosi na težnju organizma da se usklađuje s okolinom. Osnovni je cilj održati ravnotežu (ekvilibraciju) između novih i starih misaonih struktura što se postiže procesima asimilacije i akomodacije. Asimilacija je proces razumijevanja novog iskustava na temelju staroga i njegovo uključivanje u već postojeće misaone strukture. Akomodacija je mijenjanje postojećih misaonih struktura u skladu s novim iskustvima, a to se događa kada su nove informacije previše različite da bi se uklopile u postojeće strukture i na taj se način otvara put učenju nečega novoga.
Dva su temeljna oblika konstruktivističkog pristupa učenju:
- radikalni (Ernst von Glasersfeld) - znanje konstruira u glavi pojedinca stvaranjem vlastitih kognitivnih struktura na temelju novoga iskustva
- društveni (Lev Vygotski) - znanje konstruira u zajednici koja uči putem socijalnih interakcija
Radikalni konstruktivizam nastavnicima poručuje: „umjetnost poučavanja ima malo veze s prenošenjem znanja, njegova temeljna svrha mora biti poticanje umijeća učenja“ (von Glasersfeld, 1995, 192).
Konstruktivizam i e-učenje:
- Karagiorgi i Symeou (2005) razmatraju kako konstruktivizam kao teoriju učenja ugraditi u instrukcijski dizajn kroz dimenzije analize, dizajna i evaluacije, s naglaskom na aktivno, suradničko i realistično učenje.
- Wangpipatwong i Papasratorn (2008) ističu kako je konstruktivističko učenje idealan pedagoški pristup e-učenju. Oni su razvili konstruktivističko okruženje za e-učenje (CEE - constructivist e-learning environment) koje se sastoji od tri dijela: istraživanja, suradnje i konstrukcije novog znanja.
Literatura:
- Even, R., Tirosh, D. (2003). Teacher knowledge and understanding of students’ mathematical learning. U: English, L. D. (ed.), Handbook of international research in mathematics education (219-240), Mahwah, NJ: Lawrence Erlbaum Associates.
- Karagiorgi, Y., Symeou, L. (2005). Translating constructivism into instructional design: Potential and limitations. Educational Technology & Society, 8(1), 17-27.
- Von Glasersfeld, E. (1995). Radical constructivism: A way of knowing and learning. London: Falmer Press.
- Wangpipatwong, T., Papasratorn, B., (2008). „The influence of constructivist e-learning system on student learning outcomes“. U: Van Slyke, C. (ur.), Information Communication Technologies: Concepts, Methodologies, Tools, and Applications, Volume 1 (1109-1121), Hershey & London: IGI Global.
2. Strategija učenja otkrivanjem
uskoro
3. George Polya - heuristička metoda i model rješavanja problema
uskoro
4. Alan Schoenfeld - model rješavanja problema
uskoro
5. Neki modeli učenja
Temeljni model po uzoru kojeg će se razvijati naš model vođenog učenja otkrivanjem u nastavi matematike jest
1. Konceptualni model e-učenja u prirodoslovlju (Elliott, Sweeney i Irving, 2009)
To je model za e-učenje koji se temelji na konstruktivističkom pristupu te strategiji učenja otkrivanjem i strategiji rješavanja problema s primjenom u prirodoslovlju. Naglasak se stavlja na odabir objekata učenja s ciljem postizanja željenih kognitivnih ishoda učenja, a zadatke za učenike planira se kroz sljedeće etape: analiza problema, planiranje istraživanja, istraživački ciklus i rješavanje problema.
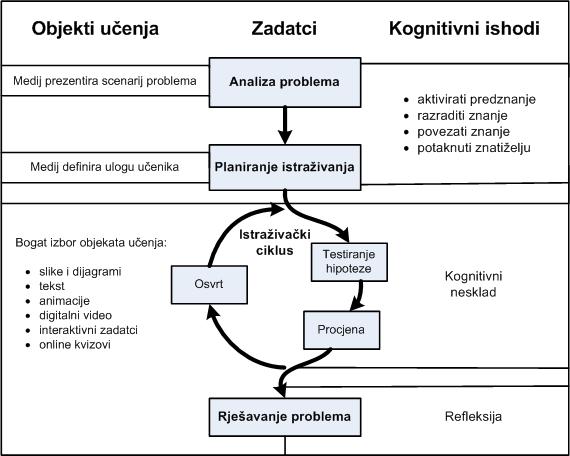
Postoje još neki modeli koji imaju dodirnih točaka s idejom razvoja novoga modela računalno vođenog učenja otkrivanjem korištenjem GeoGebre.
2. Model učenja matematike metodom rješavanja problema (Buitrago, 2006)
Ovaj model koristi tehnologiju, a naglasak se stavlja na kreativnost učenika, kritičko mišljenje, nezavisno učenje, grupni rad, sposobnost evaluacije rezultata, proučavanje pogrešaka i povezivanje nastavnih sadržaja.

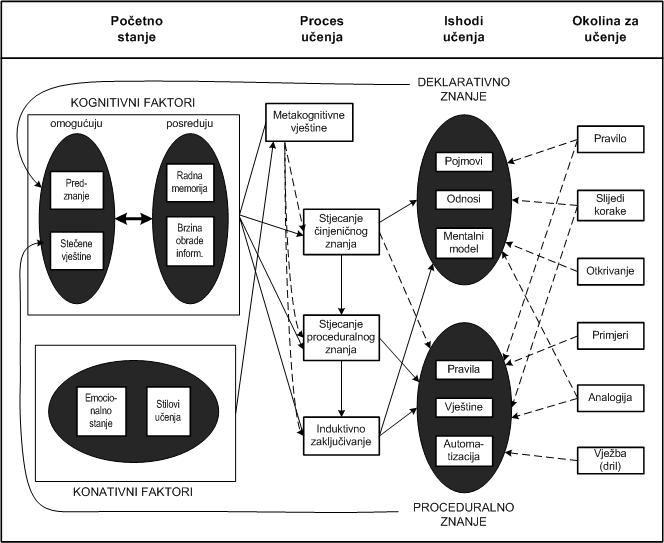
3. Funkcionalni model učenja (Shute, 1992)
Ovaj model razmatra početno stanje učenika, procese učenja i željene ishoda učenja. Postignuti ishodi učenja odražavaju razlike u procesu učenja, ali i u konativnim procesima, poznavanju strukture i metakognitivnim vještinama posredovanim procesom učenja. U radu autorice raspravljaju se različita okruženja za učenje kao i implikacije za dizajn računalnog okruženja za učenje.
Literatura:
- Buitrago, H. (2006). A model for teaching mathematics via problem-solving supported by technology. U: Hoyles, C. and other (eds.), Proceedings of the Seventeenth ICMI Study Conference “Technology Revisited” (66-73), Hanoi University of Technology.
- Elliott K., Sweeney K., Irving H. (2009). „A learning design to teach scientific inquiry“. U: Lockyer, L. i dr. (ur.), Handbook of Research on Learning Design and Learning Objects: Issues, Applications, and Technologies (652-675), Hershey & London: IGI Global.
- Shute, V. J. (1992). Learning processes and learning outcomes. (Report No. AL-TP-1992-0015). Air Force Systems Command, Brooks Air Force Base, Texas.