Sortiranje
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | III. Gimnazija Osijek - Informatika 2 |
| Knjiga: | Sortiranje |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | srijeda, 7. siječnja 2026., 14:17 |
Sadržaj
- 1. Sortiranje elemenata niza
- 2. Sortiranje zamjenom elemenata (eng. Exchange sort)
- 3. Sortiranje izborom najmanjeg elementa (eng. Selection sort)
- 4. Sortiranje zamjenom susjednih elemenata (Metoda mjehurića, engl. Bubble sort)
- 5. Sortiranje ubacivanjem (eng. Insertion sort)
- 6. Generiranje slučajnih brojeva
1. Sortiranje elemenata niza
Sortiranje niza je postupak kojim
se elementi niza slažu po veličini. Problem sortiranja niza često se pojavljuje
pa u programiranju postoji više algoritama za njegovo rješavanje. Oni se
razlikuju prema složenosti i učinkovitosti. Jednostavniji algoritmi su sasvim
dobri za sortiranje nizova s manjim brojem elemenata (najviše nekoliko
stotina), a za velike su nizove potrebni složeniji algoritmi (merge sort, quick sort).
Pogledajte usporebe brzina pojedinih algoritama:

2. Sortiranje zamjenom elemenata (eng. Exchange sort)
Algoritam za sortiranje zamjenom jedan je od jednostavnijih
algoritama i varijanta je Selection sorta. Učinkovit je za nizove s manjim brojem elemenata (do 500).
U prvom koraku, na prvo se mjesto dovodi najmanji broj, u drugom koraku, na drugo se mjesto dovodi najmanji od preostalih itd. Postupak se nastavlja sve dok se ne dobije potpuno sređeni niz.
Na koji način?
Postupak zamjene napravi se svaki put kad se pronađu dva elementa čiji je poredak obratan od redoslijeda sortiranja.
Vrijednost svakog elementa niza, počinjući od prvoga, uspoređuje se s vrijednosti elemenata koji dolaze iza njega. Ako je poredak dvaju elemenata koji se uspoređuju obratan od redoslijeda sortiranja, elementima se zamijene vrijednosti.
Podsjetimo se, varijablama x i y vrijednosti je moguće zamijeniti na više načina. Dva su najčešća:
- uporabom računskih radnji zbrajanja i oduzimanja
Ako su na početku dane varijable x=6 i y=4, niz naredbi
x=x+y; → x = 6 + 4 = 10, y ostaje nepromijenjen
y=x-y; → y = 10 – 4 = 6, x ostaje 10
x=x-y; → x = 10 – 6 = 4
daje vrijednosti x = 4 i y = 6.
- pomoćnom varijablom.
Ta se metoda može objasniti na sljedeći način: Na raspolaganju su dvije pune boce, jedna Coca-Cole, a druga Fante. Potrebno je Coca-Colu preliti u bocu Fante, a Fantu u bocu Coca-Cole. Jedini je način Coca-Colu preliti u pomoćnu posudu, zatim Fantu preliti u bocu Coca-Cole i na kraju Coca-Colu iz pomoćne posude preliti u bocu Fante! Taj se način primjenjuje i za zamjenu varijabli.
Promotrimo!
Ako su na početku dane varijable x=6 i y=4, niz naredbi
t=x; → vrijednost varijable x smješta se u pomoćnu varijablu t
x=y; → u varijablu x smješta se vrijednost varijable y, dakle x = 4
y=t; → u varijablu y smješta se vrijednost pomoćne varijable t, dakle y = 6
dat će vrijednosti x = 4 i y = 6.
2.1. Algoritam
Promotrimo na primjeru.
Neka su u niz A upisane ove vrijednosti:
![]()
U prvom prolasku kroz niz obave se sljedeći koraci (Prvi element uspoređuje se sa svim ostalim elementima. Kada naiđe na manji, zamjene mjesta u nizu):
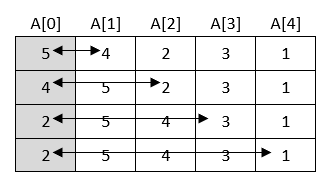
Rezultat je nakon prvog prolaska kroz niz sljedeći:
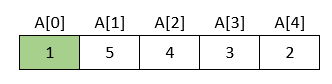
→ Najmanji element niza doveden je na prvo mjesto.
U drugom prolasku kroz polje ponavlja se isti postupak s time da se drugi element uspoređuje s ostalim elementima niza, a prvi element se ne dira.
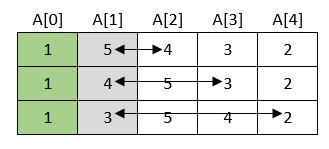
Rezultat je niz
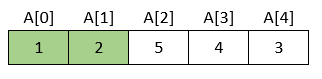
→ i drugi je element doveden na njegovo mjesto.
U trećem prolasku kroz niz uzima se treći element i njegova se vrijednost uspoređuje s vrijednostima 4. i 5. elementa.
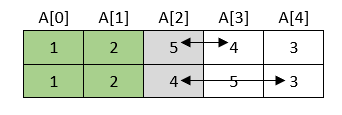
Rezultat je sljedeći:
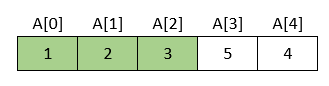
Na kraju, u četvrtom prolasku kroz niz uspoređuju se vrijednosti 4. i 5. elementa.
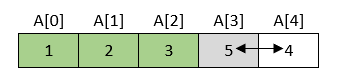
Rezultat je niz u kojem su vrijednosti elemenata poredane u rastućem redoslijedu.
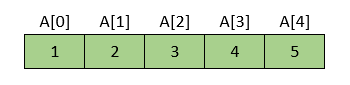
Algoritam za sortiranje na opisani način možemo zapisati na sljedeći način:
za i=1 do n-1 činitiza j=i+1 do n činiti
ako je a[i]> a[j] onda
for (j=i+1;j<n;j++)
if (a[i]>a[j])
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
2.2. Primjer
Program omogućuje upisivanje niza od najviše dvadeset elemenata, sortira ih i ispisuje u rastućem redoslijedu.
#include<stdio.h>int main()
{
int a[20],n,i,j,t;
printf("Unesi broj elemenata ");
scanf("%d",&n);
printf("Unesi elemente u polje ");
for(i=0;i<n;i++)
scanf("%d",&a[i]);
printf("\nIspis prije sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
//sortiranje selection sortom (exchange sort)
for(i=0;i<n-1;i++)
for(j=i+1;j<n;j++)
if(a[i]>a[j])
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
printf("\nIspis nakon sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
return 0;
}
3. Sortiranje izborom najmanjeg elementa (eng. Selection sort)
Prolazi se kroz polje i pronalazi najmanji element u njemu.
Kad se pronađe, zamijeni se s početnim elementom. U sljedećem koraku prvi se
element zanemari te se traži najmanji od preostalih elemenata, koji se premjesti
na drugo mjesto…
3.1. Algoritam
Promotrimo na istom primjeru kao i prethodni algoritam.Neka su u niz A upisane sljedeće vrijednosti:
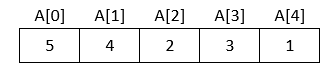
U prvom prolasku kroz niz pronađe se najmanji element koji se zatim zamijeni s prvim elementom (dakako, ako nije baš taj element najmanji).
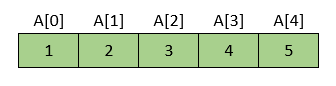
U našem primjeru, najmanji element je 1 i nalazi se na petome mjestu u nizu. Zamijenimo elemente koji se nalaze na prvome i petome mjestu.
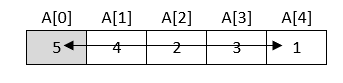
Rezultat nakon prvog prolaska kroz niz je sljedeći:
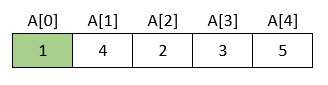
→ Najmanji element niza doveden je na prvo mjesto.
U drugom prolasku kroz polje ponavlja se isti postupak s time da prvi element ostaje na svojemu mjestu.
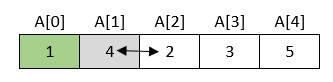
Rezultat je ovaj:
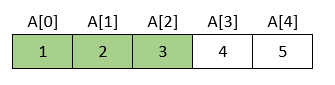
Na kraju, u četvrtom prolasku kroz niz uspoređuju se vrijednosti 4. i 5. elementa.
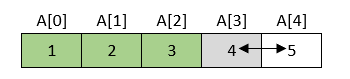
Rezultat je niz u kojem su vrijednosti elemenata poredane u rastućem redoslijedu.
{
mjesto_min=i;
za j=i+1 do n činiti
ako je a[j]<a[mjesto_min] onda
mjesto_min=j
zamijeni(a[i],a[mjesto_min])
}
Ili u programskom jeziku C:
for(i=0;i<n-1;i++){
min=i;
for(j=i+1;j<n;j++)
if (a[j]<a[min])
min=j;
t=a[i];
a[i]=a[min];
a[min]=t;
}
3.2. Primjer
Program omogućuje upisivanje niza od najviše dvadeset elemenata, sortira ih i ispisuje u rastućem redoslijedu.
#include<stdio.h>
int main()
{
int a[20],n,i,j,t,min;
printf("Unesi broj elemenata ");
scanf("%d",&n);
printf("Unesi elemente u polje ");
for(i=0;i<n;i++)
scanf("%d",&a[i]);
printf("\nIspis prije sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
//sortiranje selection sortom
for(i=0;i<n-1;i++)
{
min=i;
for(j=i+1;j<n;j++)
if (a[j]<a[min])
min=j;
t=a[i];
a[i]=a[min];
a[min]=t;
}
printf("\nIspis nakon sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
return 0;
}
3.3. Dodatni izvori
4. Sortiranje zamjenom susjednih elemenata (Metoda mjehurića, engl. Bubble sort)
Ova se metoda od prethodnih razlikuje po tome što se u bubble sortu uspoređuju susjedne vrijednosti, a ne učvršćuje se jedan element čija se vrijednost tada uspoređuje s vrijednostima preostalih elemenata.
Metodom mjehurića uspoređuju
se parovi u nizu (1. i 2.
element, 2. i 3…, predzadnji i zadnji). Rezultat takva uspoređivanja jest postavljanje najmanje (ili najveće)
vrijednosti na zadnje mjesto u nizu. U sljedećem se koraku izostavlja
zadnji element niza i prethodni se postupak ponavlja s preostalim elementima
niza.
4.1. Algoritam
Na prethodnom primjeru to izgleda ovako:
1. korak
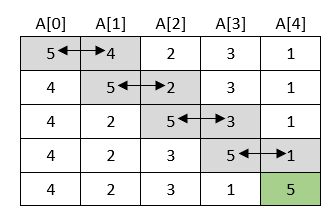
→ najveći element premješten je na zadnje
mjesto i u sljedećem se koraku izostavlja zadnji element.
2. korak
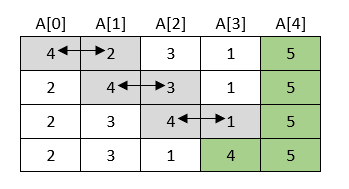
3. korak
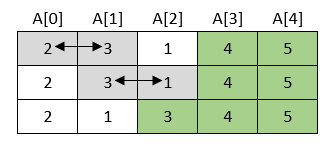
4. korak
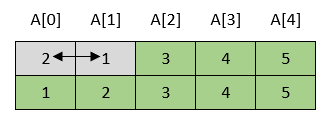
Algoritam za sortiranje metodom mjehurića je sljedeći:
za i=1 do n činitiza j=0 do n-i činiti
ako je a[j]>a[j+1] onda
zamijeni(a[j],a[j+1])
Dio programa u programskom jeziku C koji sortira niz brojeva metodom mjehurića je sljedeći:
for(i=1;i<n;i++)for(j=0;j<n-i;j++)
if (a[j]>a[j+1])
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
Ipak, taj se algoritam može malo optimizirati.
Ako uspoređivanje prestane kad se u prolasku kroz niz ne obavi nijedna zamjena, to znači da je niz posložen. Zbog kontrole zamjene uvodi se pomoćna varijabla koja može biti brojčana ili logička. Njezina se vrijednost mijenja na početku svakog prolaska kroz niz na jednu vrijednost, a ako je učinjena barem jedna zamjena, pomoćna će varijabla poprimiti drugu vrijednost. Prvi put kad se vrijednost kontrolne varijable ne promijeni tijekom prolaska kroz niz, algoritam staje (niz je sortiran).
Zbog takva načina uspoređivanja preporučuje se za sortiranje gotovo sortiranih nizova, u kojima će uspoređivanje prestati istog trenutka kad se niz sortira (za razliku od prethodne metode). To je također metoda koja se koristi za sortiranje nizova s manjim brojem elemenata.
Algoritam
i=1dok je (k<>0 ILI i==1) činiti
{
k=0
za j = 0 do n-i-1 činiti
ako je a[j]>a[j+1]
{
zamijeni(a[j],a[j+1])
k=1
}
i=i+1
}
Dio programa u programskom jeziku C koji sortira niz brojeva metodom mjehurića je sljedeći:
i=1;while (k!=0 || i==1)
{
k=0;
for (j=0;j<n-i;j++)
if (a[j]>a[j+1])
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
k=1;
}
i++;
}
4.2. Primjer
1. verzija
#include<stdio.h>
int main()
{
int a[20],n,i,j,t;
printf("Unesi broj elemenata ");
scanf("%d",&n);
printf("Unesi elemente u polje ");
for(i=0;i<n;i++)
scanf("%d",&a[i]);
printf("\nIspis prije sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
//sortiranje bubble sortom
for(i=1;i<n;i++)
for(j=0;j<n-i;j++)
if (a[j]>a[j+1])
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
printf("\nIspis nakon sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
return 0;
}
2. verzija
#include<stdio.h>
int main()
{
int a[20],n,i,j,t,k;
printf("Unesi broj elemenata ");
scanf("%d",&n);
printf("Unesi elemente u polje ");
for(i=0;i<n;i++)
scanf("%d",&a[i]);
printf("\nIspis prije sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
//sortiranje bubble sortom
i=1;
while (k!=0 || i==1)
{
k=0;
for (j=0;j<n-i;j++)
if (a[j]>a[j+1])
{
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
k=1;
}
i++;
}
printf("\nIspis nakon sortiranja\n");
for(i=0;i<n;i++)
printf("%d\t",a[i]);
return 0;
}
4.3. Dodatni izvori
5. Sortiranje ubacivanjem (eng. Insertion sort)
Ova se metoda svodi na to da niz podijelimo na dva dijela: sortirani i nesortirani dio. Na početku je nesortirani dio cijeli niz, a sortirani je dio prazan. Uzima se jedan po jedan element i smješta u sortirani dio niza, ali tako da ga se odmah stavlja na njegovo odgovarajuće mjesto. Za bolje razumijevanje pogledajte neki od videozapisa na internetu vezan za to sortiranje.
Ovaj dio programa sortira niz uporabom Insertion sorta:
//sortiranje insertion sortomfor (i=1;i<n;i++)
{
k=a[i];
for (j=i;j>0 && k<a[j-1];j--)
a[j]=a[j-1];
a[j]=k;
}
Na ovom dijelu programa možete uočiti i jednu od specifičnosti programskog jezika C, a to je da uvjet u petlji for ne mora nužno biti vezan za kontrolnu varijablu koja odbrojava broj prolaza kroz petlju. To znači da u petlji for ne moramo nužno znati broj ponavljanja unaprijed.
5.1. Dodatni izvori
6. Generiranje slučajnih brojeva
Kad trebamo više podataka, njihovo nam učitavanje može oduzeti mnogo vremena. Tada se za provjeravanje ispravnosti algoritama koristimo generatorom slučajnih brojeva.
Za korištenje generatorom slučajnih brojeva potrebno je uključiti biblioteku stdlib.h. Funkcija rand() generira slučajan broj iz intervala [0, RAND_MAX]. Broj RAND_MAX je najveći slučajni broj koji se može generirati. Ovisi o računalu, a lako ga je provjeriti naredbom printf("%d", RAND_MAX);.
Vrijednost RAND_MAX je obično 327687, no to nije pravilo.Isprobajmo generator slučajnih brojeva s pomoću jednostavnog programa:
#include<stdlib.h>#include<stdio.h>
int main()
{
printf("%d", rand());
return 0;
}
Prepišite ga i pokrenite nekoliko puta. Uočit ćete da program svaki put ispisuje isti broj. Da bismo to izbjegli, trebamo inicijalizirati generator slučajnih brojeva srand(). Kako bismo izbjegli da srand() vraća uvijek jednak niz slučajnih brojeva, možemo iskoristiti funkciju time() koja vraća broj sekundi proteklih od 1. siječnja 1970. Ta se funkcija nalazi u biblioteci time.h.
Isprobajte sada sljedeći program i uočite razliku.
#include<stdlib.h>#include<stdio.h>
#include<time.h>
int main()
{
srand(time(NULL));
printf("%d", rand());
return 0;
}
Vrlo često trebamo generirati slučajne brojeve iz točno određenog intervala brojeva. Naredba rand()%10 generirat će broj iz intervala od 0 do 9 (uključujući i rubne brojeve), naredba rand()%101 broj iz intervala od 0 do 100, a naredba rand()%401+100 ispisat će slučajni broj iz intervala [100, 500]. Općenito, želimo li generirati slučajne brojeve iz intervala [min,max] možemo to učiniti sljedećom formulom:
rand()%(max + 1 - min) + min