Ucrtaj na kraju još i izoliranu točku .
Slikaj rezultat i postavi sliku na Teams, poveznica:
1A
1B
Koordinatni sustav u ravnini
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | Računalstvo 1 |
| Knjiga: | Koordinatni sustav u ravnini |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | četvrtak, 26. prosinca 2024., 20:53 |
Opis
1. Koordinatne osi
Položaj neke točke na brojevnom pravcu određen je jednim realnim brojem, koordinatom te točke. Za položaj točke u koordinatnoj ravnini potrebno je znati dva broja, njezine dvije koordinate, apscisu i ordinatu.
Postavimo međusobno okomito dva brojevna pravca, i y, tako da imaju zajedničko ishodište . Na brojevnom pravcu pozitivni su brojevi zdesna ishodištu, a na brojevnom pravcu pozitivni su brojevi smješteni iznad ishodišta, što je na slici naznačeno strelicama. Pravce i zovemo koordinatnim osima. Pravac je os apscisa, pravac os ordinata. Na ovaj je način određen sustav koji nazivamo pravokutni koordinatni sustav ili Kartezijev sustav.
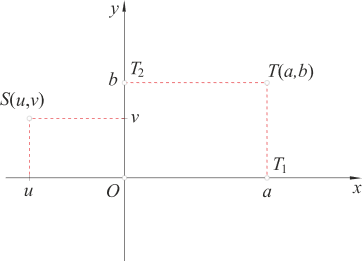
2. Koordinate točke
Točku koja je određena uređenim parom realnih brojeva odredit ćemo na sljedeći način: na osi apscisa odredimo točku s koordinatom , a na osi ordinata točku s koordinatom . Točkama i položimo pravce paralelno koordinatnim osima. Oni se sijeku u točki . Ta je točka pridružena uređenom paru dvaju realnih brojeva i . Kažemo da su i koordinate točke T. Broj njezina je apscisa, a broj njezina ordinata.
Odaberemo li u koordinatnoj ravnini neku točku , povlačenjem paralela s koordinatnim osima odredit ćemo na njima sjecišta s koordinatama i , a uređeni par bit će pridružen točki . Brojevi i su apscisa i ordinata točke .
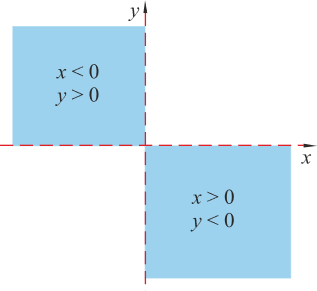
3. Kvadranti
Koordinatne osi, pravci i dijele ravninu u četiri područja koja se zovu kvadranti. Kvadrante karakteriziraju predznaci koordinata njihovih točaka.
U I. kvadrantu obje su koordinate svake točke pozitivni brojevi, u II. apscise svih točaka su negativne, a ordinate pozitivne.
U III. kvadrantu svaka točka ima obje negativne koordinate, a za točke IV. kvadranta apscise su pozitivni, a ordinate negativni brojevi.
4. Primjeri
Primjeri riješenih zadataka
4.1. Primjer 1.
Primjer 1: Odredimo skup svih točaka \( T(x,y) \) ravnine za čije koordinate vrijedi \( x \cdot y<0 \)
Rješenje: Ako je umnožak koordinata neke točke negativan broj, koordinate te točke su brojevi suprotnih predznaka. Uvjet zadovoljavaju sve točke II. i IV. kvadranta, ali bez točaka na koordinatnim osima. Kada bi uvjet glasio , skupu bi pripadale i točke na koordinatnim osima.
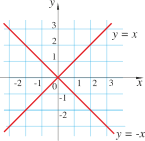
4.2. Primjer 2.
Primjer 2. Odredimo skup svih točaka ravnine čije su koordinate vezane uvjetom \( x^2-y^2=0 \) .
Rješenje: Uvjet \( x^2-y^2=0 \) ekvivalentan je uvjetu \( (x-y) \cdot (x+y) =0 \).
Slijedi \( x-y=0 \Rightarrow x=y \) ili \( x+y=0 \Rightarrow x=-y \) .
Jednadžbom su izdvojene točke ravnine tipa \( (x,x) , (x,-x) \).
5. Zadatak
Zadatak:
Nacrtaj u bilježnicu koordinatni sustav.
Ucrtavaj redom u koordinatni sustav točke te svaku sljedeću spoji s prethodnom: , , , , , , , , , , , , , , , , ,