Brojevni sustavi i kodovi
| Sitio: | CARNET - Arhiva 2021 Loomen |
| Curso: | Digitalna logika |
| Libro: | Brojevni sustavi i kodovi |
| Imprimido por: | Invitado |
| Día: | Thursday, 5 de March de 2026, 19:50 |
1. Brojevni sustavi
Brojevni sustav je zajednički naziv za skup pravila pomoću kojih se jednoznačno zapisuju brojevi. Pravila opisuju kako se brojevi zapisuju (znamenke), kao i kako se zapis jednoznačno tumači. Važno svojstvo brojevnog sustava je mogućnost zapisa svih (ili barem prirodnih) brojeva.
1.1. Dekadski brojevni sustav
U decimalnom brojevnom sustavu ima deset znamenaka: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9, što znači da se svi brojevi od nula do devet mogu prikazati s jednom znamenkom.
To su jednoznamenkasti brojevi. Najveći broj koji se može napisati s jednom znamenkom je devet.
Općenito se može reći da najveći broj koji se može
napisati s n znamenaka iznosi 10n- 1. Položaj znamenke u bilo kojem broju naziva se brojno mjesto.
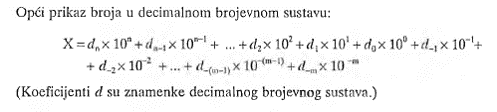
1.2. Binarni brojevni sustav
Binarni brojevni sustav ima samo dvije znamenke: 0 i 1. Najveći broj koji se uopće može napisati s n znamenaka iznosi 2n- 1.

1.3. Oktalni brojevni sustav
Oktalni brojevni sustav ima osam znamenaka: 0, 1, 2, 3, 4, 5, 6 i 7. Najveći broj koji se može napisati s n znamenki je 8n- l .

1.4. Pretvaranje iz dekadskog sustava u ostale brojevne sustave
Broj u dekadskom sustavu se dijeli s bazom. Ostatak pišemo desno a rezultat cjelobrojnog dijeljenja lijevo kao što je prikazano na slici.
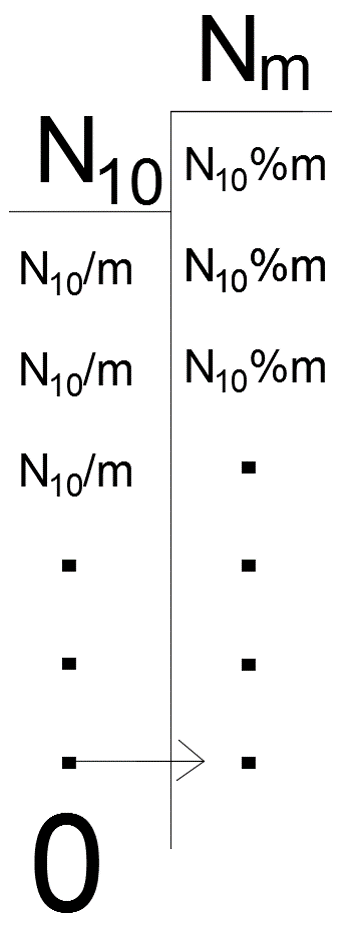
Nakon što smo pretvorili cijelobrojni dio možemo pretvoriti i dio nakon zareza.
0,134 -> u bazu 7 -> 0,063
0,134 * 7 = 0,938
0,938 * 7 = 6,566 // 6 prebacujemo gore, a ostaje nam 0,566
0,566 * 7 = 3,962 // 3 prebacujemo gore
1.5. Pretvaranje iz ostalih brojevnih sustava u dekadski
Kada se pretvara iz ostalih brojevnih sustava u dekadski znamenku množimo s bazom potenciranom na mjesto na kojem se ta znamenka nalazi.
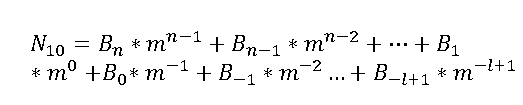
1.6. Video Brojevni sustavi
2. Kodovi
BCD kod
Excess 3 kod
Aikenov kod
Grayev kod
Kodovi za otkrivanje pogreške
2.1. BCD kod
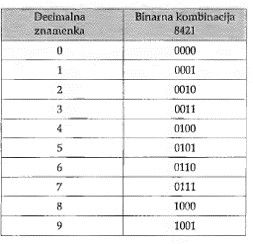
Za kodiranje decimalnih znamenaka u BCD kodu (skraćeno od engl. Binary Coded Decimal) koristi se prvih deset kombinacija prirodnog binarnog četverobitnog niza. To znači da se svaka decimalna znamenka prikazuje pripadnim binarnim brojem.
Stoga se ovaj kod ponekad naziva i prirodni binarno decimalni kod ili kraće NBCD -kod (od engl. Natural Binary Coded Decimal).
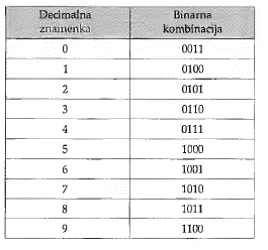
2.2. Excess 3 kod
Za kodiranje decimalnih znamenaka u excess-3 kodu (skraćeno XS-3 kodu) koristi se srednjih deset kombinacija binarnog četverobitnog niza, a odbacuju se prve tri i zadnje tri kombinacije.
Excess-3 kod razlikuje se od BCD koda i po tome što nije težinski, ali je samokomplementirajući (engl, selfcomplemented). To znači da se komplement bilo koje znamenke dobije zamjenom nula s jedinicama i jedinica s nulama. Osim toga, u excess-3 kodu ne pojavljuju se kombinacije sa sve četiri nule niti sve četiri jedinice,
što može biti korisno za otkrivanje prekida u prijenosu podataka.
2.3. Aikenov kod
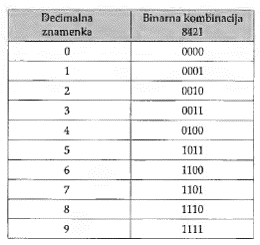
U Aikenovu kodu koristi se prvih pet i zadnjih pet kombinacija četverobitnog niza, a odbacuje se srednjih šest kombinacija.
Kod je samokomplementirajući i težinski, s težinama mjesta 2421.
2.4. Grayev kod
Karakteristika je Grayeva koda, koji nije težinski, da se svaka kombinacija razlikuje od prethodne za samo jedan bit. Grayev kod temelji se na reflektiranom (zrcalnom) binarnom brojevnom sustavu. Stoga taj kod spada u skupinu reflektiranih kodova (engl. reflected codes).
Brojevi reflektiranog binarnog brojevnog sustava dobiju se na sljedeći način: znamenke 0 i 1 napisu se jedna ispod druge. Ispod njih se povuče zamišljena zrcalna crta i ispod nje napisu znamenke 1 i 0 kao zrcalna slika. Sada se ispred gornjih znamenaka dodaju nule, a ispod donjih jedinice.
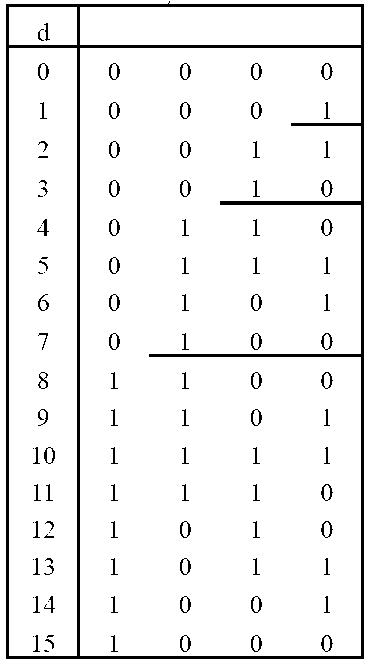
Ako se ispod njih povuče nova zrcalna crta i ispod nje napisu reflektirane kombinacije pa se gornjima dodaju nule, a donjima jedinice, dobije se osam trobitnih kombinacija. Na taj način može se dobiti broj kombinacija po želji.
Za Grayev kod koristi se prvih deset kombinacija četverobitnog niza.
2.5. Parni paritet
Vrlo često se za siguran prijenos kodiranih podataka koristi metoda pariteta. Radi se o tome da se svakoj binarnoj kombinaciji kojom se prikazuje digitalni podatak dodaje jedan bit. Dodatni bit naziva se paritetni bit (engl. parity bit).
Paritetni bit dodaje se tako da u kombinaciji s povećanim brojem bitova uvijek postoji isključivo paran broj jedinica (parni paritet, engl. even parity) ili neparan broj jedinica (neparni paritet, engl. odd parity). Pogreška u prijenosu koja uzrokuje promjenu jednog bita mijenja paritet jedinica u podatku što, upućuje na pogrešku.
Slovo A kodirano u ASCII kodu je 10 0001. Ova kombinacija ima paran broj jedinica. Stoga je dodatni paritetni bit jednak 0 pa je A u ASCII kodu s parnim paritetom 01000001, što opet daje paran broj jedinica.
Slovo C kodirano ASCII kodom je 1000011, što daje neparan broj jedinica. Stoga je paritetni bit 1 pa je C u ASCII kodu s parnim paritetom 11000011, što daje ukupno paran broj jedinica.
2.6. Neparni paritet
Kod s neparnim paritetom.
A u ASCII kodu je 1000001, dakle sadrži paran broj jedinica. Prema tome, u kodu s neparnim paritetom A će biti 11000001, što daje ukupno neparan broj jedinica.
C u ASCII kodu je 100 0011, dakle sadrži neparan broj jedinica. U kodu s neparnim paritetom C će biti 0100 0011, što daje opet neparan broj jedinica.
2.7. Hammingov kod
Ispitni broj od i bita može pokazati pogrešku na ukupno (2i -1) bitnih mjesta. Sto je veći broj znakovnih bitova, potreban je veći broj ispitnih bitova.
Kako se ukupna kodna kombinacija sastoji od z znakovnih i i ispitnih bitova, da bi se u takvom kodu moglo utvrditi mjesto pogreške mora biti ispunjen uvjet:
2i >= Z+i +1
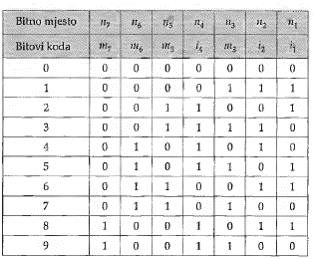
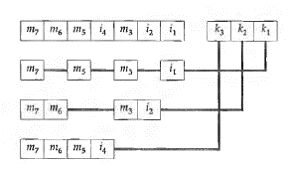
Znakovni bitovi m7, m6, m5 i m3 služe za prikaz dekadnih znamenki, a ispitni bitovi i4, i2 i i1, su dodatni bitovi za paritet. Ispitivanje pariteta izvodi se tri puta. U prvom ispitivanju ispituju se bitovi m7, ms, m3 i i1, u drugom ispitivanju bitovi m 7, m6, m3 i i2 te u trećem ispitivanju bitovi m 7, m6, m5 i i4.
Ako je ispitivanje na paritet uspješno, tj. u ispitivanoj kombinaciji je paran broj jedinica, onda se rezultat ispitivanja označava s 0. Kad ispitivanje na paritet nije uspješno, tj. kad je u ispitivanoj
kombinaciji neparan broj jedinica, onda se rezultat ispitivanja označava s 1.
Na taj način dobije se trobitna kombinacija k bitova koja označava bitno mjesto n na kojemu se nalazi pogreška. Ako su sva tri ispitivanja uspješna, svi k bitovi su 0, što znači da nema pogreške u kodnim bitovima.