Uvod u programiranje
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | Moodle_2011 |
| Knjiga: | Uvod u programiranje |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | ponedjeljak, 5. siječnja 2026., 10:53 |
Opis
Osnove digitalnih računala i brojevnih sustava.
Uvod u programiranje
1. lekcija: Digitalna računala i brojevni sustaviO 1. lekciji |
|
Aktivnosti
Ishodi učenja za cjelinuPo završetku 1. lekcije polaznici će moći:
LiteraturaObavezna literatura Soulie, J. (2010). C++ Language tutorial. cplusplus.com. Preuzeto 28.03.2011. s http://www.cplusplus.com/files/tutorial.pdf Izborna literatura Osnove programiranja u C++. |
Uvod
Pojam računalo ili kompjuter predstavlja uređaj koji izvršava određene radnje prema programima koje izrađuje čovjek. Sastavni dijelovi računala su sklopovlje ili hardver (hardware) i programi (software) s pripadajućom dokumentacijom za njihovo korištenje. Program najčešće predstavlja opis operacija koje računalo treba izvršiti, a zapisuje se formalnim jezikom koji se naziva programski jezik. Računala bi na osnovi funkcioniranja mogli podijeliti na analogna i digitalna. Obrada kontinuiranih elektroničkih signala se obavlja analognim računalima. Digitalna računala obrađuju, prenose i pamte diskretne elektroničke signale. Ovi signali u jednom trenutku mogu imati samo jedno od dva moguća stanja prikazana znamenkama (digits) 0 i 1. Bitno je napomenuti da programere i korisnike računala ne zanimaju sami elektronički signali, već poruka koju oni prenose – digitalna informacija.
Brojevni sustav u kojem postoje samo dvije znamenke naziva se binarni brojevni sustav. Svaka znamenka toga sustava naziva se bit (binary digit), a može imati samo dvije vrijednosti 0 ili 1. Binarno kodirane informacije u računalu mogu biti kodirane kao naredbe (ili instrukcije) koje računalo treba izvršiti ili kao neki smisleni podatak.
Digitalna računala
Sastavni dijelovi digitalnog računala su prikazani na slici 1.1. Centralna procesorska jedinica (CPU) kontrolira izvršenje programa i aritmetičko logičkih operacija. CPU je izveden kao jedinstven integrirani elektronički sklop (čip) i naziva se mikropreocesor. Često se koristi naziv procesor, bilo da se radi o mikroprocesoru ili o skupini čipova koji obavljaju funkcije CPU. Procesor izvršava programski kod te je stoga uobičajeno programe koji se izvršavaju u računalu nazivati procesima. Prema tome, proces predstavlja program u izvršenju.
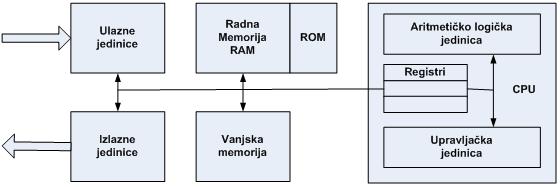
Slika 1.1. Pojednostavljeni prikaz digitalnog računala
Radna memorija pamti digitalne informacije za vrijeme dok je računalo u operativnom stanju. U memoriji se nalazi programski kod i podaci s kojima operira procesor na temelju naredbi koje su sadržane u programskom kodu. Memorija je napravljena od poluvodičkih elemenata u koje procesor može upisati i iz kojih može očitati stanje digitalne informacije i naziva se RAM (Random Access Memory). S gledišta programera RAM predstavlja linearno uređen prostor u kojem se istovremeno može pristupiti grupi od 8 bita (1 Byte) digitalne informacije. Položaj ove temeljne memorijske ćelije se označava prirodnim brojem i predstavlja adresu memorijske lokacije. Također jedan manji dio memorije je napravljen od poluvodičkih elemenata koji mogu trajno pamtiti digitalnu informaciju i naziva se ROM (Read Only Memory). U ROM-u je upisan program koji služi za pokretanje osnovnih funkcija računala. U samom procesoru je ugrađeno nekoliko manjih memorijskih jedinica koje se nazivaju registri. Registri služe za privremeni smještaj programskog koda i podataka iz radne memorije, te rezultata aritmetičko-logičkih operacija koje se izvršavaju u samo procesoru. Broj bita koji može biti pohranjen u jednom registru naziva se riječ (word) procesora. Kod današnjih PC računala riječ procesora sadrži 32 bita (4 bajta) ili 64 bita (8 bajtova), pa se kaže da su to 32-bitna ili 64-bitna računala.
Vanjska memorija služi za trajno pohranjivanje podataka, a za pohranu se koriste magnetski, optički i elektronički mediji (tvrdi diskovi, optički diskovi, flash memorije ...).
Ulazne jedinice služe za unos podataka (tipkovnica, miš, mikrofon, skener...).
Izlazne jedinice služe za prikaz informacija korisniku računala (monitori, pisači, zvučnici ...).
Računalo u radnom stanju održava poseban program koji se naziva operacijski sustav (operation system). Ovaj program obavlja osnovne funkcije računala: inicijalizaciju računala i priključenih vanjskih jedinica pri uključenju samog računala (paljenju), kontrolu i redosljed izvođenja programa, kontrolu uporabe memorije, prijem, pohranjivanje i obradu podataka, vremesku raspodjelu funkcija računala, itd. Operacijski sustav nije nužno jedinstven program, već se sastoji od više programskih cjelina. On se jednim dijelom trajno nalazi u ROM memoriji računala, te se programi s ovakvim svojstvom nazivaju rezidentni programi. Svi ostali programi se prije izvršenja moraju upisati u memoriju računala. Podjela softvera se može izvršiti na sistemski i aplikativni. U sistemski softver spadaju programi operacijskog sustava, razni jezični procesori (interpreteri, kompajleri, emulatori ...), programi za testiranje programa (debugger), servisni i uslužni programi, te razni pomoćni programi (matematički, statistički, baze podataka i uređivači teksta ...). Aplikativni softver predstavljaju različiti korisnički programi (programi za pristup i obradu podataka iz različitih baza, programi za određeni hardver i sl.). Programi koji studenti obrađuju u sklopu ovog kolegija spadaju u aplikativni softver.
Brojevni sustavi
Svi smo mi od malih nogu naučeni upotrebljavati decimalne brojeve za izražavanje količine. Ova nomenklatura, koja nama izgleda jako logična starim Rimljanima nimalo nije bila logična. Za njih je svaki simbol za izraz nekog broja uvijek predstavljao istu vrijednost:
|
I - |
1 |
|
II - |
2 |
|
III - |
3 |
|
IV - |
4 |
|
V - |
5 |
Ako se obrati pažnja, svaki "I" znak uvijek predstavlja vrijednost 1, gdjegod bio postavljen. Međutim, u dekadskome sustavu stvari baš i nisu takve. Kada se napiše dekadski simbol "1", ne govori se baš uvijek o vrijednosti 1, na primjer:
|
1 - |
I |
|
10 - |
X |
|
100 - |
C |
U ovim slučajevima, simbol "1" nema uvijek vrijednost 1 ("I" kod rimskih brojeva). Na primjer, u drugome slučaju simbol "1" predstavlja vrijednost 10 (što je znak "X" u rimskoj notaciji), a u trećemu slučaju simbol "1" predstavlja vrijednost 100 (C).
Još jedan primjer:
Broj 275 nije ekvivalentan: 2 + 7 + 5, već se može raščlaniti kao 200 + 70 + 5: te stoga, prvi znak 2 je ekvivalent 200 (2 × 100), drugi znak 7 je ekvivalent 70 (7 × 10), te naposljetku zadnji znak odgovara vrijednosti 5 (5 × 1).
Sve prijašnje može se matematički predstaviti na jako jednostavan način. Na primjer, za predstavljanje vrijednosti 182736 može se pretpostaviti da je svaka znamenka produkt sebe same pomnožene s 10x, gdje x odgovara mjestu na kojemu se znamenka nalazi, počevši od desna s 100, iza kojega slijedi 101, 102, itd. (slika 1.2.).
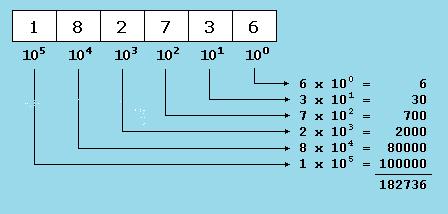
Slika 1.2. Dekadski brojevni sustav
Ovaj brojevni sustav nam je svima poznat i predstavlja dekadski brojevni sustav koji ima bazu 10 jer postoji 10 različitih znamenki (od 0 do 9):
0 1 2 3 4 5 6 7 8 9 .
Oktalni brojevni sustav
Kao što dekadski brojevni sustav ima bazu 10 oktalni brojevni sustav uključuje samo znamenke od 0 do 7:
0 1 2 3 4 5 6 7 ,
pa je stoga, baza sustava 8. U C++ oktalni brojevi imaju karakteristiku da uvijek počinju znamenkom 0. Pogledajmo kako bismo pisali nekoliko prvih brojeva u oktalnom brojevnom sustavu:
|
octal |
decimal |
octal |
decimal |
||
|
0 |
0 |
(zero) |
011 |
9 |
(nine) |
|
01 |
1 |
(one) |
012 |
10 |
(ten) |
|
02 |
2 |
(two) |
013 |
11 |
(eleven) |
|
03 |
3 |
(three) |
014 |
12 |
(twelve) |
|
04 |
4 |
(four) |
015 |
13 |
(thirteen) |
|
05 |
5 |
(five) |
016 |
14 |
(fourteen) |
|
06 |
6 |
(six) |
017 |
15 |
(fifteen) |
|
07 |
7 |
(seven) |
020 |
16 |
(sixteen) |
|
010 |
8 |
(eight) |
021 |
17 |
(seventeen) |
Broj 17 prikazan je kao broj 021 . Može se upotrijebiti ista shema na oktalni brojevni sustav kao i za dekadski sustav, vodeći računa da je baza oktalnoga brojevnog sustava 8. Razmotrimo na primjer oktalni broj 071263 (slika 1.3.).
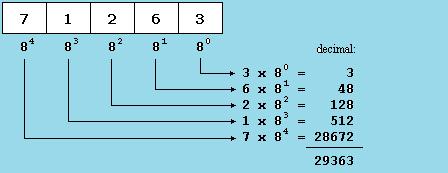
Slika 1.3. Pretvorba oktalnog broja u dekadski
Iz navedenoga primjera slijedi da se oktalni broj 071263 u dekadskome brojevnom sustavu prikazuje kao 29363.
Heksadekadski brojevni sustav
Kao što dekadski brojevi imaju 10 različitih znamenki za prezentaciju i oktalni brojevi imaju 8, heksadekadski brojevi imaju 16 različitih znamenki: brojeve od 0 to 9 i slova A, B, C, D, E i F koja služe za predstavljanje 16 različitih potrebnih simbola:
|
hexadecimal |
decimal |
hexadecimal |
decimal |
||
|
0 |
0 |
(zero) |
0x9 |
9 |
(nine) |
|
0x1 |
1 |
(one) |
0xA |
10 |
(ten) |
|
0x2 |
2 |
(two) |
0xB |
11 |
(eleven) |
|
0x3 |
3 |
(three) |
0xC |
12 |
(twelve) |
|
0x4 |
4 |
(four) |
0xD |
13 |
(thirteen) |
|
0x5 |
5 |
(five) |
0xE |
14 |
(fourteen) |
|
0x6 |
6 |
(six) |
0xF |
15 |
(fifteen) |
|
0x7 |
7 |
(seven) |
0x10 |
16 |
(sixteen) |
|
0x8 |
8 |
(eight) |
|||
Još jednom možemo upotrijebiti istu metodu za preračunavanje broja iz neke baze u drugu bazu (slika 1.4.).
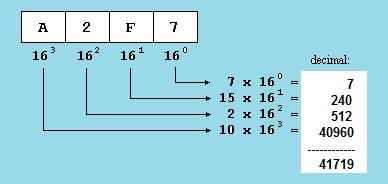
Slika 1.4. Pretvorba heksadekadskog broja u dekadski
U C++ heksadekadski brojevi imaju karakteristiku da uvijek počinju znamenkama 0x.
Binarni brojevni sustav
Oktalni i heksadekadski brojevi imaju veliku prednost u svijetu bitova pred decimalnim brojevima, još pogotovo time što su njihove baze (8 i 16) potencije broja 2 (23 i 24), što omogućava lakšu konverziju u binarni sustav. Na primjer, pretpostavimo da želimo proslijediti sljedeću binarnu sekvencu u broj s drugom bazom:
11011010 .
Da bismo je prebacili u dekadski sustav (slika 1.5.) morali bismo provesti matematičku operaciju sličnu onoj upotrijebljenu u prijašnjem primjeru, za konverziju iz heksadekadskog ili oktalnog.
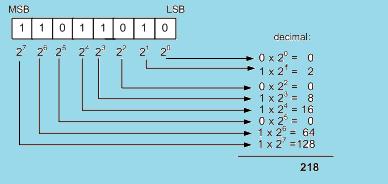
Slika 1.5. Pretvorba binarnoga broja u dekadski
Rezultat pretvorbe je decimalni broj 218 . Također u binarnome nizu bitan je redoslijed bitova, kratica LSB ( Least Significant Bit ) označava bit najmanjeg značaja, a MSB ( Most Significant Bit ) označava bit najvećeg značaja.
Međutim, da bi proslijedili ovu sekvencu u oktalni sustav potrebno je samo nekoliko sekundi, a dovoljno je samo baciti pogled: kako je 8 u biti 23, potrebno je samo razdvojiti binarne vrijednosti u grupe od tri člana počevši s desna na lijevo:
11 011 010
te nadalje ih prevesti u bazu po 8 i to svaku grupu zasebno:
11 011 010
3 3 2
što za rezultat daje broj 332. Isti proces može se izvršiti unazad u svrhu prosljeđivanja iz oktalnog u binarni sustav.
Da bi se izvodile operacije heksadekadskim brojevima potrebno je istim procesom izdvajanja binarnih vrijednosti u grupe od četiri člana s desna na lijevo (16 = 24):
1101 1010
D A
Stoga, binarni izraz 11011010 može se prezentirati u C++ kao 218 (dekadski), kao 0332 (oktalno) ili kao 0xDA (heksadekadsko).
Kako se danas računala temelje na bajtovima sastavljenim od 8 binarnih bitova, što se najpogodnije predstavlja heksadekadskim brojevima, heksadekadski kod je specijalno zanimljiv u računalskoj znanosti. Kada se skupinom od četiri bita radi kao cjelinom, često se koristi naziv nibl (nibble).
Pretvaranje dekadskoga broja u binarni najlakše je napraviti preko ostataka dijeljenja s 2 kao u sljedećem primjeru:
|
57 : 2 = 28 |
|
1 |
|
28 : 2 = 14 |
|
0 |
|
14 : 2 = 7 |
|
0 |
|
7 : 2 = 3 |
|
1 |
|
3 : 2 = 1 |
|
1 |
|
1 : 2 = 0 |
|
1 |
Sada rezultat dobijemo tako što čitamo ostatke dijeljenja odozdo prema gore, 111001 (binarno), 57 (dekadski).
|
Aktivnost - Domaći rad! Riješi domaći rad i odgovore pošalji u word ili pdf formatu do 05.04.2011. putem e-maila. |
