Osnovni pojmovi o funkciji
| Sjedište: | CARNET - Arhiva 2021 Loomen |
| E-kolegij: | Kvadratna funkcija |
| Knjiga: | Osnovni pojmovi o funkciji |
| Otisnuo/la: | Gost (anonimni korisnik) |
| Datum: | petak, 15. studenoga 2024., 05:20 |
Opis
Sadržaj i aktivnosti poglavlja
U ovom poglavlju ponovit ćete osnovne pojmove o funkcijama. Podsjetit ćete se definicije funkcije, što su to domena i kodomena funkcije, te graf funkcije. Ponovit ćete pojam linearne funkcije.
Sadržaj i aktivnosti poglavlja
U ovom poglavlju ponovit ćete osnovne pojmove o funkcijama. Podsjetit ćete se definicije funkcije, što su to domena i kodomena funkcije, te graf funkcije. Ponovit ćete pojam linearne funkcije.
Ciljevi:
Učenici će nakon ovog poglavlja moći
- definirati funkciju
- definirati graf
- razlikovati domenu i kodomenu
- rješavati zadatke s linearnom funkcijom
Aktivnosti:
- proučite lekcije u ovom poglavlju
- naučite pojmove definirane u lekciji
- proučite navedene primjere
- riješite kviz
Osnovno o funkcijama
Funkcija je preslikavanje koje svakom elementu skupa A pridruži točno jedan element skupa B.
Skup A nazivamo domena (područje definicije), a skup B kodomena (područje vrijednosti).
Zapisujemo:
Mi ćemo promatrati funkcije za koje je domena i kodomena podskup skupa realnih brojeva. Takve funkcije nazivamo realnim funkcijama.
Primjer 1.
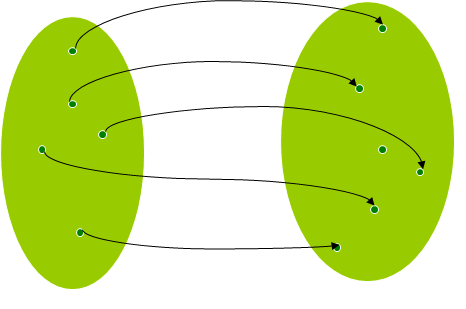
Prikazuje li slika funkciju?
Odgovor 1.
Nije funkcija jer:
• u skupu A ima nepridruženih elemenata
• jednom elementu iz A pridružena su dva elementa iz B
Graf funkcije
Graf $$\Gamma _{f}$$ funkcije f je skup svih točaka $$\left ( x,f\left ( x \right ) \right ) $$ za sve x iz domene $$D_{f}$$ funkcije f:
.
Graf neke funkcije:
Primjer 2.
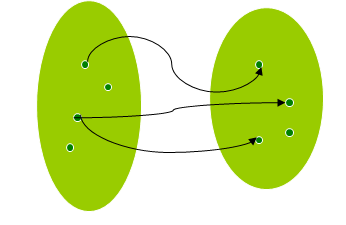
Prikazuje li slika graf funkcije?
Odgovor 2.
Na slici nije prikazan graf funkcije jer sa istom koordinatom x imamo tri različite točke (jednom elementu iz domene pridružena su tri elementa iz kodomene).
Linearna funkcija
Funkcija $$f:R\rightarrow R $$ zadana formulom $$f\left ( x \right )=ax+b$$ je polinom prvog stupnja ili linearna funkcija.
Njezina domena i kodomena je skup realnih brojeva.
Graf linearne funkcije je pravac. Broj a naziva se koeficijent smjera, a b je odsječak na osi y. Pravac je određen sa svoje dvije točke.
Primjeri:
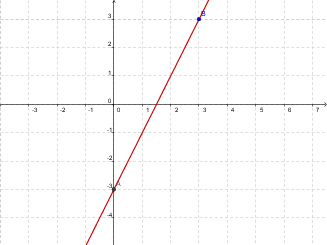
a) Nacrtajmo graf funkcije $$ f\left ( x \right )=2x-3$$.
Uzmimo da je $$x_{1}=0$$ i $$x_{2}=3$$
Tada je $$y_{1}=2\cdot 0-3=-3$$ i $$y_{2}=2\cdot 3-3=3$$.
Graf je prikazan na slici:
b) Odredi linearnu funkciju $$f\left ( x \right )=ax+b$$, ako je: $$f\left ( 3 \right )=-1, f\left ( -3 \right )=3$$ .
Slijedi:
Riješimo li ovaj sustav jednadžbi dobivamo: $$ b=1, a=-\frac{2}{3}$$
tj. tražena funkcija je: $$f\left ( x \right )=-\frac{2}{3}x+1 $$