Volumen
Volumen je fizička veličina kojom opisujemo koliko tijela zauzimaju prostora. Označavamo ga sa V.
Mjerna jedinica za obujam je kubni metar, m3

Kubni metar je jedinica za obujam kocke brida 1 metar.
V = a ∙ a ∙ a
V = 1m ∙ 1m ∙ 1 m = 1 m3
Evo i nekih drugih manjih jedinica za volumen:
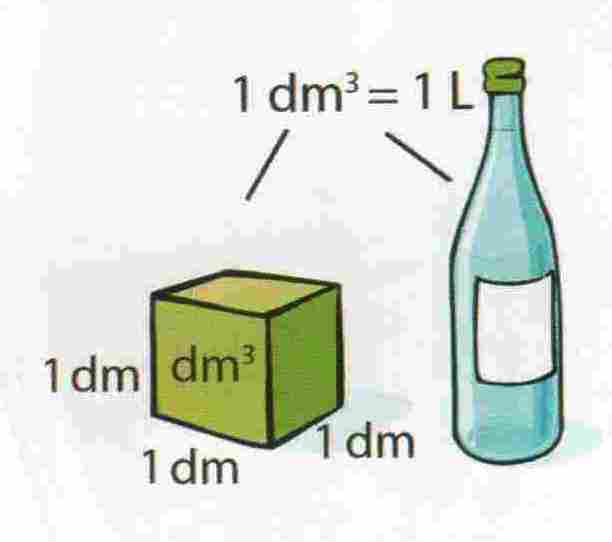
Kubni decimetar, dm3, volumen je kocke stranice 1 dm
Kubni centimetar, cm3, volumen je kocke stranice 1 cm
Kubni milimetar, mm3, volumen je kocke stranice 1 mm
Odnosi između mjernih jedinica za obujam:
1 m3 = 1 m ∙ 1 m ∙ 1 m = 10 dm ∙ 10 dm ∙ 10 dm
1 m3 = 1000 dm3
1 dm3 = 1 dm ∙ 1 dm ∙ 1 dm = 10 cm ∙ 10 cm ∙ 10 cm
1 dm3 = 1 000 cm3
1 dm3 = 1/1 000 m3 = 0,001 m3
1 cm3 = 1 cm ∙ 1 cm ∙ 1 cm = 10 mm ∙ 10 mm ∙ 10 mm
1 cm3 = 1 000 mm3
1 cm3 = 1/1 000 000 m3 = 0,000 001 m3
1 cm3 = 1/1 000 dm3 = 0,001 dm3
1 mm3 = 1/1 000 cm3 = 0,001 cm3
1 mm3 = 1/1 000 000 dm3 = 0,000 001 dm3
1 mm3 = 1/1 000 000 000 m3 = 0,000 000 001 m3
Za tekućine je često u uporabi jedinica litra. Označuje se sa L ili l.
1 L = 1 dm3
1 L = 1 dL
1 m L = 1 cm3

Određivanje volumena geometrijskih tijela
a) Izravno mjerenje
Kvadar se može potpuno ispuniti kockicama brida 1 cm. Volumen svake te kockice iznosi 1 cm3 . Kockice se prebroje.
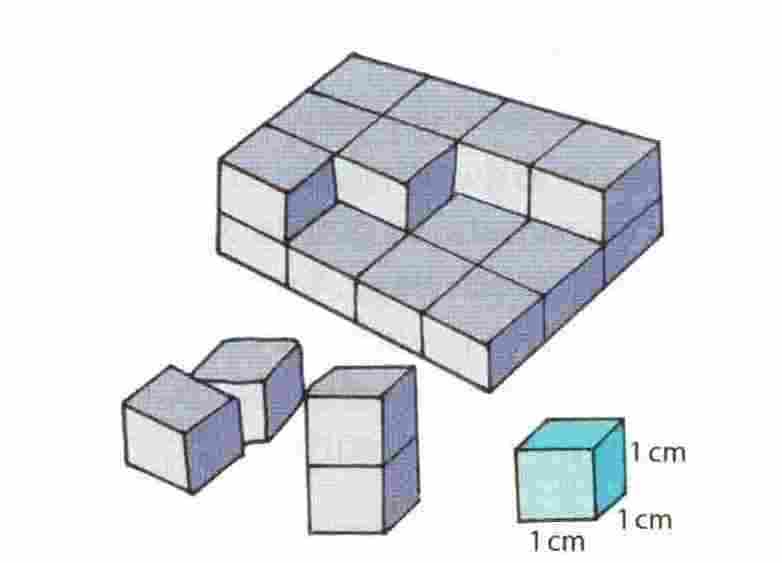
Ukupno imamo 24 kockice, pa je volumen kvadra V = 24 cm3
b) Računanje
Isti rezultat se dobije ako se izmjere, a zatim pomnože stranice kvadra.
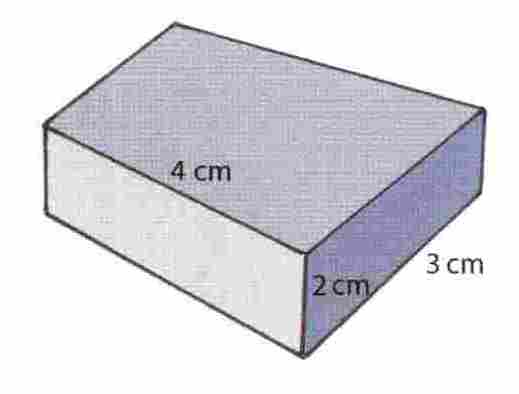
V = a ∙ b ∙ c
V = 4 cm ∙ 3 cm ∙ 2 cm
V = 24 cm3
Mjerenje volumena nepravilnih tijela
- određuje se pomoću menzure. Potrebno je prisjetiti se načina mjerenja obujma pomoću menzure. Važno je da se razina vode u menzuri drži u ravnini očiju i da se odčita njezin najniži položaj.
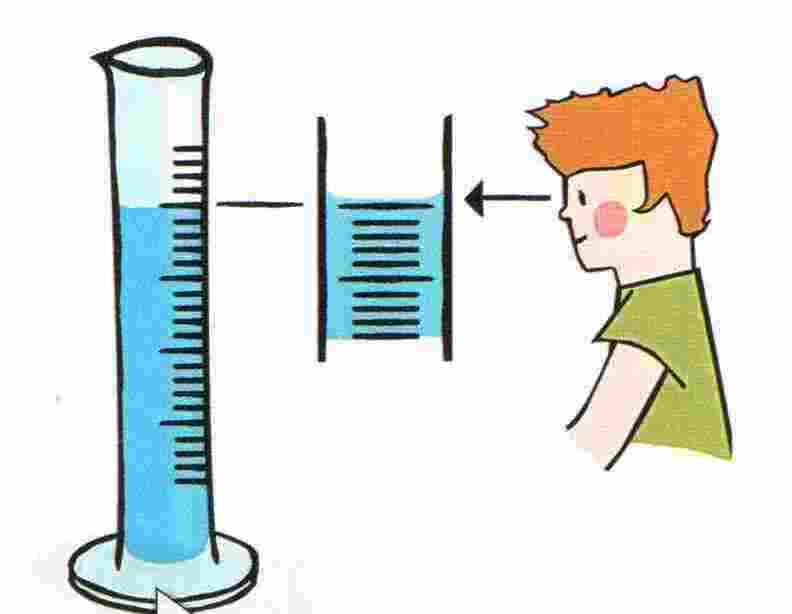
Primjer: Mjerenje volumena plastelinske loptice
Kada se pomoću menzure želi odrediti volumen nepravilnog tijela, najprije se izmjeri volumen količine vode V1 . Zatim se uroni u menzuru nepravilno tijelo te se izmjeri ukupni volumen vode i uronjenog nepravilnog tijela V2 . Razlika tih vrijednosti je volumen nepravilnog tijela
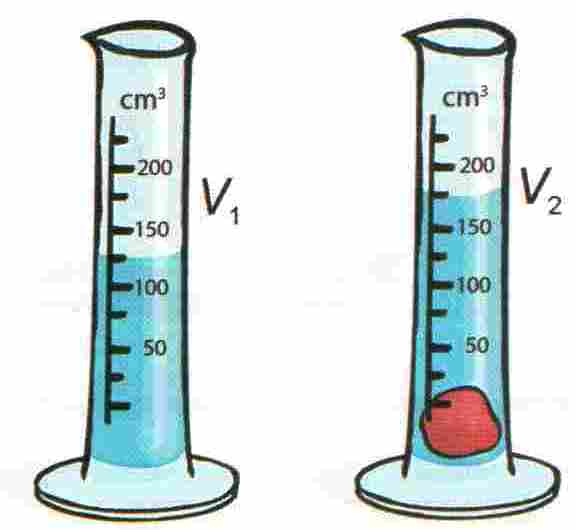
V = V2 - V1
V1 = 125 cm3
V2 = 175 cm3
V = ?
V = V2 - V1
V = 175 cm3 - 125 cm3
V = 50 cm3