Brojevni sustavi i kodovi
2. Kodovi
2.7. Hammingov kod
Ispitni broj od i bita može pokazati pogrešku na ukupno (2i -1) bitnih mjesta. Sto je veći broj znakovnih bitova, potreban je veći broj ispitnih bitova.
Kako se ukupna kodna kombinacija sastoji od z znakovnih i i ispitnih bitova, da bi se u takvom kodu moglo utvrditi mjesto pogreške mora biti ispunjen uvjet:
2i >= Z+i +1
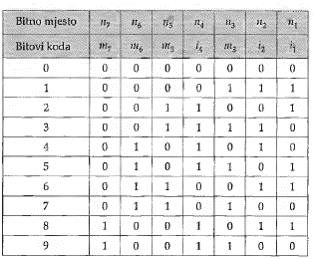
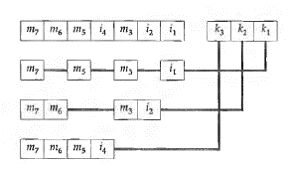
Znakovni bitovi m7, m6, m5 i m3 služe za prikaz dekadnih znamenki, a ispitni bitovi i4, i2 i i1, su dodatni bitovi za paritet. Ispitivanje pariteta izvodi se tri puta. U prvom ispitivanju ispituju se bitovi m7, ms, m3 i i1, u drugom ispitivanju bitovi m 7, m6, m3 i i2 te u trećem ispitivanju bitovi m 7, m6, m5 i i4.
Ako je ispitivanje na paritet uspješno, tj. u ispitivanoj kombinaciji je paran broj jedinica, onda se rezultat ispitivanja označava s 0. Kad ispitivanje na paritet nije uspješno, tj. kad je u ispitivanoj
kombinaciji neparan broj jedinica, onda se rezultat ispitivanja označava s 1.
Na taj način dobije se trobitna kombinacija k bitova koja označava bitno mjesto n na kojemu se nalazi pogreška. Ako su sva tri ispitivanja uspješna, svi k bitovi su 0, što znači da nema pogreške u kodnim bitovima.