III. Gimnazija Osijek - Informatika 2

Na prethodnom primjeru to izgleda ovako:

1. korak

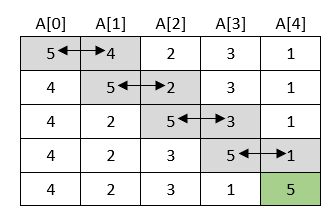
→ najveći element premješten je na zadnje mjesto i u sljedećem se koraku izostavlja zadnji element.

2. korak

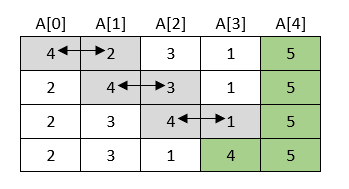
3. korak

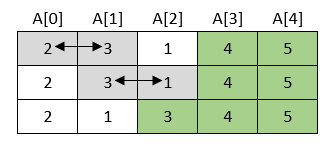
4. korak

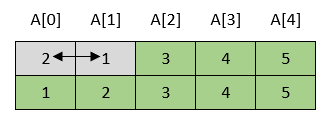
Algoritam za sortiranje metodom mjehurića je sljedeći:

za i=1 do n činiti
    za j=0 do n-i činiti
        ako je a[j]>a[j+1] onda
          zamijeni(a[j],a[j+1])

 

Dio programa u programskom jeziku C koji sortira niz brojeva metodom mjehurića je sljedeći:

for(i=1;i<n;i++)
     for(j=0;j<n-i;j++)
           if (a[j]>a[j+1])
           {
                t=a[j];
                a[j]=a[j+1];
                a[j+1]=t;
           }

Ipak, taj se algoritam može malo optimizirati.

Ako uspoređivanje prestane kad se u prolasku kroz niz ne obavi nijedna zamjena, to znači da je niz posložen. Zbog kontrole zamjene uvodi se pomoćna varijabla koja može biti brojčana ili logička. Njezina se vrijednost mijenja na početku svakog prolaska kroz niz na jednu vrijednost, a ako je učinjena barem jedna zamjena, pomoćna će varijabla poprimiti drugu vrijednost. Prvi put kad se vrijednost kontrolne varijable ne promijeni tijekom prolaska kroz niz, algoritam staje (niz je sortiran).

Zbog takva načina uspoređivanja preporučuje se za sortiranje gotovo sortiranih nizova, u kojima će uspoređivanje prestati istog trenutka kad se niz sortira (za razliku od prethodne metode). To je također metoda koja se koristi za sortiranje nizova s manjim brojem elemenata.

Algoritam

i=1
dok je (k<>0 ILI i==1) činiti
{
     k=0
     za j = 0 do n-i-1 činiti
           ako je a[j]>a[j+1]
           {
                zamijeni(a[j],a[j+1])
                k=1
           }
     i=i+1
}

 Dio programa u programskom jeziku C koji sortira niz brojeva metodom mjehurića je sljedeći:

     i=1;
     while (k!=0 || i==1)
     {
           k=0;
           for (j=0;j<n-i;j++)
                if (a[j]>a[j+1])
                {
                      t=a[j];
                      a[j]=a[j+1];
                      a[j+1]=t;
                      k=1;
                }   
           i++;
     }