Uvod u programiranje
Osnove digitalnih računala i brojevnih sustava.
Brojevni sustavi
Svi smo mi od malih nogu naučeni upotrebljavati decimalne brojeve za izražavanje količine. Ova nomenklatura, koja nama izgleda jako logična starim Rimljanima nimalo nije bila logična. Za njih je svaki simbol za izraz nekog broja uvijek predstavljao istu vrijednost:
|
I - |
1 |
|
II - |
2 |
|
III - |
3 |
|
IV - |
4 |
|
V - |
5 |
Ako se obrati pažnja, svaki "I" znak uvijek predstavlja vrijednost 1, gdjegod bio postavljen. Međutim, u dekadskome sustavu stvari baš i nisu takve. Kada se napiše dekadski simbol "1", ne govori se baš uvijek o vrijednosti 1, na primjer:
|
1 - |
I |
|
10 - |
X |
|
100 - |
C |
U ovim slučajevima, simbol "1" nema uvijek vrijednost 1 ("I" kod rimskih brojeva). Na primjer, u drugome slučaju simbol "1" predstavlja vrijednost 10 (što je znak "X" u rimskoj notaciji), a u trećemu slučaju simbol "1" predstavlja vrijednost 100 (C).
Još jedan primjer:
Broj 275 nije ekvivalentan: 2 + 7 + 5, već se može raščlaniti kao 200 + 70 + 5: te stoga, prvi znak 2 je ekvivalent 200 (2 × 100), drugi znak 7 je ekvivalent 70 (7 × 10), te naposljetku zadnji znak odgovara vrijednosti 5 (5 × 1).
Sve prijašnje može se matematički predstaviti na jako jednostavan način. Na primjer, za predstavljanje vrijednosti 182736 može se pretpostaviti da je svaka znamenka produkt sebe same pomnožene s 10x, gdje x odgovara mjestu na kojemu se znamenka nalazi, počevši od desna s 100, iza kojega slijedi 101, 102, itd. (slika 1.2.).
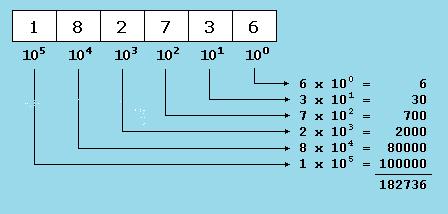
Slika 1.2. Dekadski brojevni sustav
Ovaj brojevni sustav nam je svima poznat i predstavlja dekadski brojevni sustav koji ima bazu 10 jer postoji 10 različitih znamenki (od 0 do 9):
0 1 2 3 4 5 6 7 8 9 .