CARNET - Arhiva 2021 Loomen

Oktalni i heksadekadski brojevi imaju veliku prednost u svijetu bitova pred decimalnim brojevima, još pogotovo time što su njihove baze (8 i 16) potencije broja 2 (2³ i 2⁴), što omogućava lakšu konverziju u binarni sustav. Na primjer, pretpostavimo da želimo proslijediti sljedeću binarnu sekvencu u broj s drugom bazom:

11011010 .

Da bismo je prebacili u dekadski sustav (slika 1.5.) morali bismo provesti matematičku operaciju sličnu onoj upotrijebljenu u prijašnjem primjeru, za konverziju iz heksadekadskog ili oktalnog.

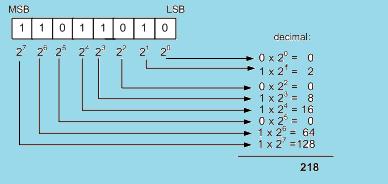
Slika 1.5. Pretvorba binarnoga broja u dekadski

Rezultat pretvorbe je decimalni broj 218 . Također u binarnome nizu bitan je redoslijed bitova, kratica LSB ( Least Significant Bit ) označava bit najmanjeg značaja, a MSB ( Most Significant Bit ) označava bit najvećeg značaja.

Međutim, da bi proslijedili ovu sekvencu u oktalni sustav potrebno je samo nekoliko sekundi, a dovoljno je samo baciti pogled: kako je 8 u biti 2³, potrebno je samo razdvojiti binarne vrijednosti u grupe od tri člana počevši s desna na lijevo:

11   011   010

te nadalje ih prevesti u bazu po 8 i to svaku grupu zasebno:

11   011   010

 3       3       2

što za rezultat daje broj 332. Isti proces može se izvršiti unazad u svrhu prosljeđivanja iz oktalnog u binarni sustav.

Da bi se izvodile operacije heksadekadskim brojevima potrebno je istim procesom izdvajanja binarnih vrijednosti u grupe od četiri člana s desna na lijevo (16 = 2⁴):

1101 1010

    D      A

Stoga, binarni izraz 11011010 može se prezentirati u C++ kao 218 (dekadski), kao 0332 (oktalno) ili kao 0xDA (heksadekadsko).

Kako se danas računala temelje na bajtovima sastavljenim od 8 binarnih bitova, što se najpogodnije predstavlja heksadekadskim brojevima, heksadekadski kod je specijalno zanimljiv u računalskoj znanosti. Kada se skupinom od četiri bita radi kao cjelinom, često se koristi naziv nibl (nibble).

Pretvaranje dekadskoga broja u binarni najlakše je napraviti preko ostataka dijeljenja s 2 kao u sljedećem primjeru:

57 : 2 = 28
1
28 : 2 = 14
0
14 : 2 = 7
0
7 : 2 = 3
1
3 : 2 = 1
1
1 : 2 = 0
1

Sada rezultat dobijemo tako što čitamo ostatke dijeljenja odozdo prema gore, 111001 (binarno), 57 (dekadski).

Aktivnost - Domaći rad! Riješi domaći rad i odgovore pošalji u word ili pdf formatu do 05.04.2011. putem e-maila.