Primjer 2
Odredimo jednadžbu pravca paralelnog s pravcem y = -2x, a koji dira kružnicu (x + 2)2 + (y - 7)2 = 5.
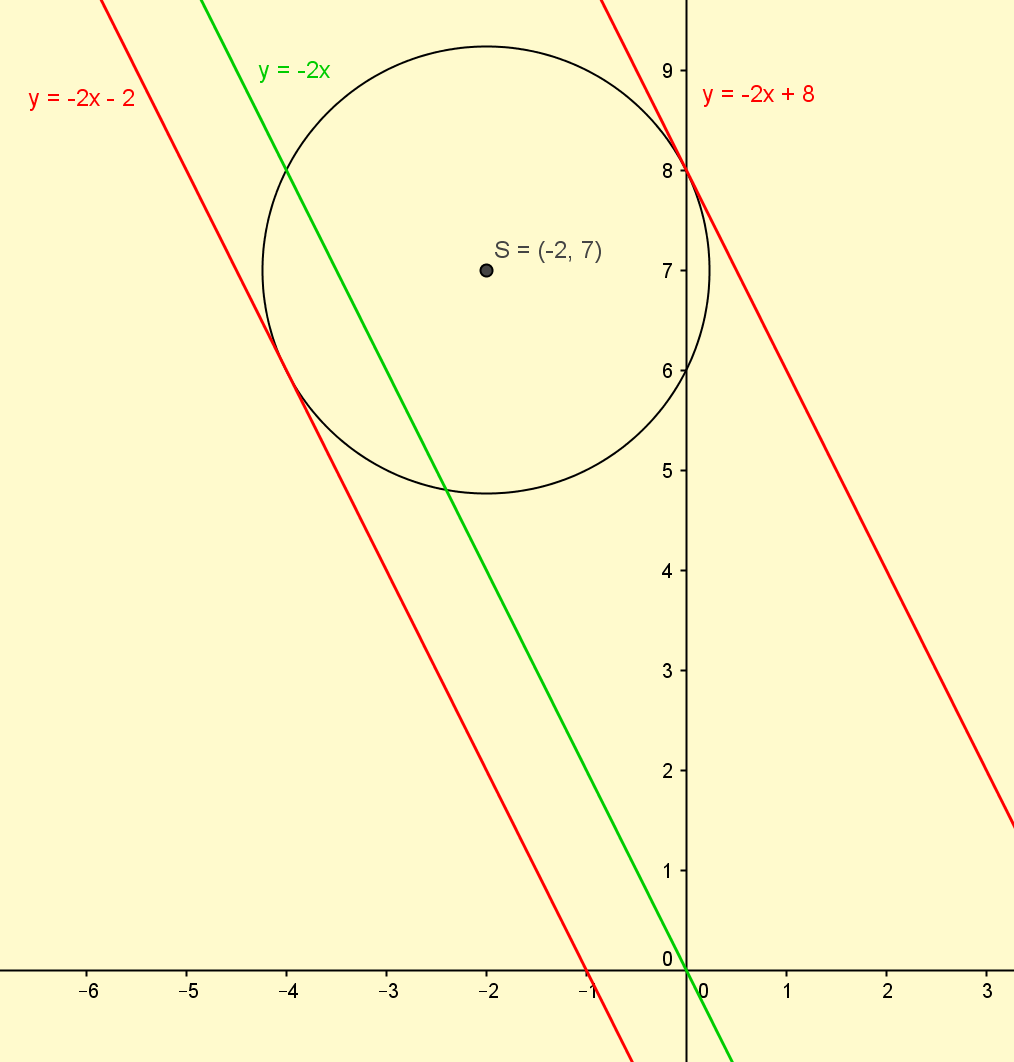
Ako je tangenta paralelna sa zadanim pravcem, onda je njena jednadžba
y = -2x + l
Trebamo riješiti sustav i to tako da ima jedno dvostruko rješenje.
y = -2x
(x + 2)2 + (y - 7)2 = 5
Dakle, diskriminanta treba biti jednaka nuli.
5x2 + (32 - 4l)x + l2 - 14l + 48 = 0 \( \Rightarrow \) (32 - 4l)2 - 20(l2 - 14l + 48) = 0 \( \Rightarrow \)
l2 - 6l - 16 =0 \( \Rightarrow \) l1 = -2 i l2 = 8
Tražene tangente imaju sljedeće jednadžbe y = -2x - 2 i y = -2x + 8.
Zadnji puta izmijenjeno: nedjelja, 17. srpnja 2016., 22:57