Tema Ime Opis
Jednadžba kružnice Knjiga Sadržaj

Jednadžba kružnice u koordinatnom sustavu.
Knjiga Ciljevi i aktivnosti

Na slici je prikazana meta sa strelicom u središtu

 

   Ciljevi ove lekcije

 

Nakon ove lekcije moći ćete:

  • Crtati kružnicu iz njezine jednadžbe
  • Određivati kružnicu iz njezine opće jednadžbe
  • Odrediti jednadžbu kružnice zadane trima točkama

Na slici je prikazan varioc sa zaštitnom maskom na licu kako radi.

 

   Aktivnosti ove lekcije

 

  • Proučite sadržaj ove lekcije
  • Riješite zadatke iz Vježbi
  • Odgovorite na pitanja u Testu 1
  • Predajte Zadaću 1
  • Sudjelujte u diskusiji Pitanja i nedoumice
  • Međusobno komunicirajte u Brbljaonici (svaki dan u 18 sati)
Knjiga Kružnica u koordinatnom sustavu

Kružnica je svuda oko nas. Ona budi ljudski interes oduvijek. Mnogi čuveni matematički zadaci vezani su uz kružnicu i krug.

Što je kružnica?

Kružnica je skup točaka T ravnine koje su jednako udaljene od jedne čvrste točke – središta S Na slici je nekoliko kružnica koje tvore cvijet.kružnice.

Udaljenost točke T od središta S zove se polumjer ili  radijus kružnice.

Definiciju kružnice možemo zapisati u obliku jednakosti |ST|=r.

 

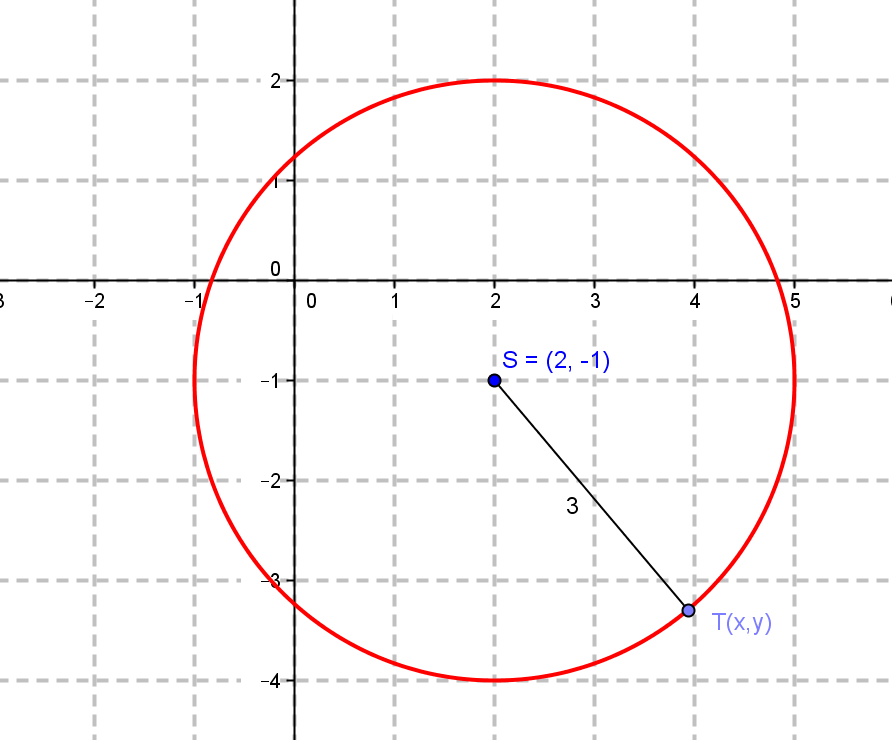
Primjer 1.

Odredimo skup svih točaka ravnine čije udaljenosti od točke S(2, -2) iznose 3 jedinice.

Neka je T(x, y) bilo koja od traženih točaka. Njezina udaljenost od točke S(2, -2) mora biti 3.

Prisjetimo se formule za izračunavanje udaljenosti točaka u koordinatnom sustavu.

|TS|= $$ \sqrt{\left(x-2\right)^{2} +\left(y+2\right)^{2}}=3$$

Na slici je kružnica sa središtem S(2, -1) i polumjerom 3

Kvadrirajmo gornju jednadžbu:

(x-2)2 + (y+2)2 = 9

Ova jednadžba predstavlja jednadžbu kružnice čije je središte u točki S(2, -2), a polumjer joj je 3.

 

                                                                                 

Knjiga Jednadžba kružnice u općem položaju

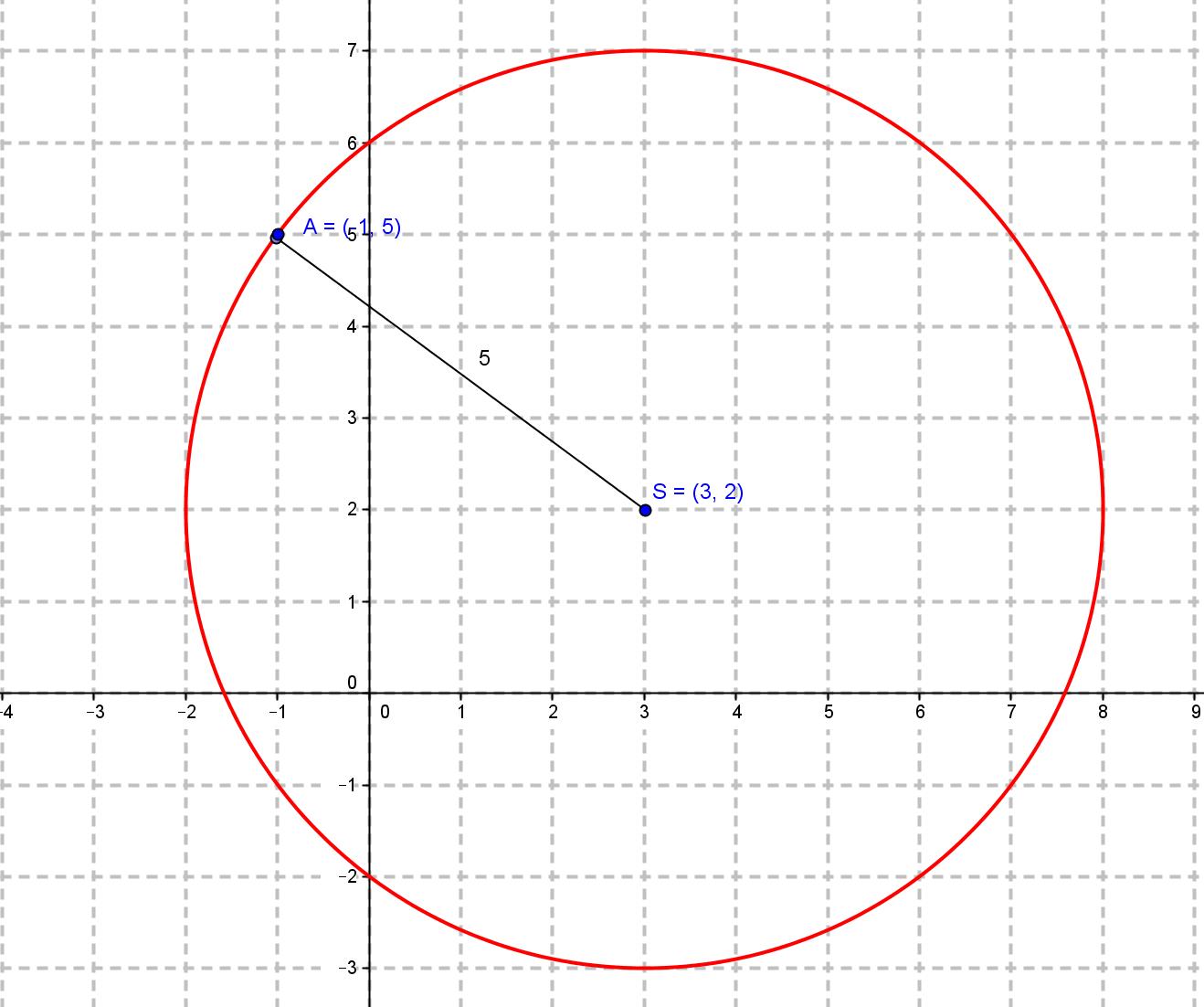
Odredimo sada jednadžbu kružnice u općem obliku. Neka je njezino središte točka S(p, q), a duljina polumjera kružnice neka je r. Za bilo koju točku     T(x, y) te kružnice vrijedi |ST|=r, odnosno

 $$ \sqrt{(x-p)^{2} +(y-q)^{2}}=r$$

Nakon kvadriranja dobijemo

(x – p)2 + (y - q)2 =r2

Kažemo da je to jednadžba kružnice u općem položaju.

Ako je središte kružnice u ishodištu koordinatnog sustava S(0, 0), jednadžba kružnice tada glasi:

 x2 + y2 = r2  

Ova se kružnica zove središnja ili centralna kružnica.

Primjer 2.

Odredimo jednadžbu kružnice čije je središte u točki S(3, 2), a prolazi točkom A(-1,5).

Potrebno je odrediti polumjer kružnice. Na slici je kružnica sa središtem S(3,2) i točkom A(-1, 5)

On je jednak udaljenosti točaka S i A:

Zato je jednadžba kružnice

(x-3)2 + (y-2)2 = 25
Knjiga Kružnica koja dodiruje koordinatne osi

Primjer 3.

Kružnica koja dodiruje koordinatne osi. Odredimo jednadžbu kružnice koja prolazi točkom A(2,1) i dodiruje obje koordinatne osi.

Točka A se nalazi u prvom kvadrantu, što znači da i naša kružnica ima središte u istom kvadrantu. Središte je točka S(p,q) i ona je od  osi jednako udaljena, tj p=q=r.

Jednadžba te kružnice je

 (x-r)2 + (y-r)2 = r2

Zato jer prolazi točkom A(2,1), njene koordinate moraju zadovoljavati danu jednadžbu

(2-r)2 + (1-r)2 = r2

Riješimo se zagrada, zbrojimo dobiveno…

            r2 -6r +5=0

Rješenja ove kvadratne jednadžbe su r1 = 1 i r2 =5. Imamo dakle dvije kružnice kojima su jednadžbe:

k1 … (x - 1)2 + (y - 1)2 = 1

k2  … (x - 5)2 + (y - 5)2 = 25.

 
Stranica Rješenje zadatka

Ako niste uspjeli samostalno riješiti zadatak pogledajte rješenje.
Stranica Vježba 1

Zadaci za uvježbavanje prve lekcije.
Knjiga Opća jednadžba kružnice

Opća jednadžba kružnice Ax2+Ay2+Dx+Ey+F=0
Stranica Vježba 2

Riješite zadane zadatke.
Knjiga Zadavanje kružnice

Kružnicu možemo zadati na nekoliko načina.
Pravac i kružnica Knjiga Sadržaj


U ovom dijelu ćemo razmotriti u kojim sve međusobnim položajima se mogu naći pravac i kružnica,

kako računski doći do njihovih zajedničkih točaka, ukoliko one postoje naravno.


Upoznat ćemo se sa uvjetom dodira pravca i kružnice, te jednadžbom tangente u točki kružnice.
Knjiga Ciljevi i aktivnosti

  • Ciljevi ove lekcije:

  •  Nakon ove lekcije ćete moći.
  •  - odrediti u kakvom su međusobnom položaj pravac i kružnica
  •  - odrediti jednadžbu tangente u točki kružnice
  •  - odrediti jednadžbu kružnice iz točke na kružnicu


  • Aktivnosti u ovoj lekciji:

  •  - pročitajte  poglavlja
  •  - proučite primjere
  •  - poigrajte se geogebrom
  •  - riješite vježbu 3
  •  - predajte zadaću 2
  •  - sudjelujte u raspravi
Knjiga Presjek pravca i kružnice

Pravac i kružnica se mogu pojaviti u tri različita  međusobna položaja. 
Stranica Primjer 2

Što ako znamo koeficijent smjera ili odsječak na osi y tražene tangente?
Knjiga Uvjet dodira

Kako bi pravac bio tangenta kružnice, on mora zadovoljavati uvjet dodira.
Stranica Primjer 3

Određivanje tangente na kružnicu s poznatim koeficijentom smjera.
Knjiga Tangenta i normala u točki na kružnici

Normala je pravac koji prolazi diralištem tangente i okomit je na nju.
Knjiga Jednadžba tangente iz točke izvan kružnice

Iz točke izven kružnice mogu e povući dvije tangente.
Stranica Vježba 3

Zadatci za uvježbavanje