Jednadžba kružnice u općem položaju
Odredimo sada jednadžbu kružnice u općem obliku. Neka je njezino središte točka S(p, q), a duljina polumjera kružnice neka je r. Za bilo koju točku T(x, y) te kružnice vrijedi |ST|=r, odnosno
$$ \sqrt{(x-p)^{2} +(y-q)^{2}}=r$$
Nakon kvadriranja dobijemo
(x – p)2 + (y - q)2 =r2
Kažemo da je to jednadžba kružnice u općem položaju.
Ako je središte kružnice u ishodištu koordinatnog sustava S(0, 0), jednadžba kružnice tada glasi:
x2 + y2 = r2
Ova se kružnica zove središnja ili centralna kružnica.
Odredimo jednadžbu kružnice čije je središte u točki S(3, 2), a prolazi točkom A(-1,5).
Potrebno je odrediti polumjer kružnice. 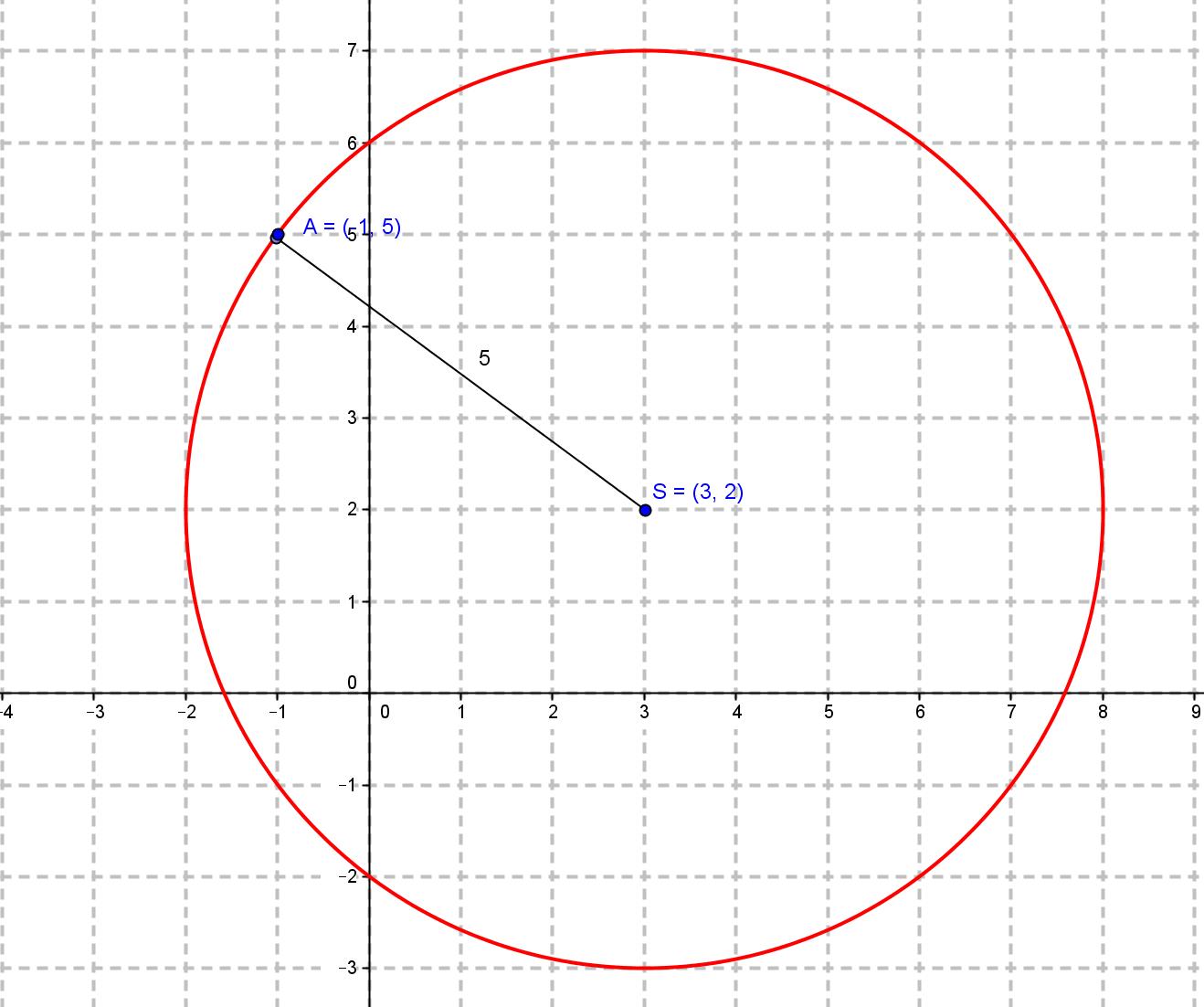
On je jednak udaljenosti točaka S i A:
Zato je jednadžba kružnice
(x-3)2 + (y-2)2 = 25
Jednadžba kružnice u općem položaju
Odredimo sada jednadžbu kružnice u općem položaju. Neka je njezino središte točka S(p, q), a duljina polumjera kružnice neka je r.
Pokušajmo do jednadžbe kružnice doći uz pomoć geogebre:
https://www.geogebra.org/m/fqyzzA4C
Pogledajmo sada, kako se dolazi do jednadžbe kružnice:
Za bilo koju točku T(x, y) te kružnice vrijedi |ST|=r, odnosno
![]()
Nakon kvadriranja dobijemo
(x – p)2 + (y - q)2 =r2
Kažemo da je to jednadžba kružnice u općem položaju.
Ako je središte kružnice u ishodištu koordinatnog sustava S(0, 0), jednadžba kružnice tada glasi:
x2 + y2 = r2
Ova se kružnica zove središnja ili centralna kružnica.