Kružnica koja dodiruje koordinatne osi
Kružnica koja dodiruje koordinatne osi. Odredimo jednadžbu kružnice koja prolazi točkom A(2,1) i dodiruje obje koordinatne osi.
Točka A se nalazi u prvom kvadrantu, što znači da i naša kružnica ima središte u istom kvadrantu. Središte je točka S(p,q) i ona je od osi jednako udaljena, tj p=q=r.
Jednadžba te kružnice je
(x-r)2 + (y-r)2 = r2
Zato jer prolazi točkom A(2,1), njene koordinate moraju zadovoljavati danu jednadžbu
(2-r)2 + (1-r)2 = r2
Riješimo se zagrada, zbrojimo dobiveno…
r2 -6r +5=0
Rješenja ove kvadratne jednadžbe su r1 = 1 i r2 =5. Imamo dakle dvije kružnice kojima su jednadžbe:
k1 … (x - 1)2 + (y - 1)2 = 1
k2 … (x - 5)2 + (y - 5)2 = 25.
Kružnica koja dodiruje koordinatne osi
Kružnica koja dodiruje koordinatne osi. Odredimo jednadžbu kružnice koja prolazi točkom A(2,1) i dodiruje obje koordinatne osi.
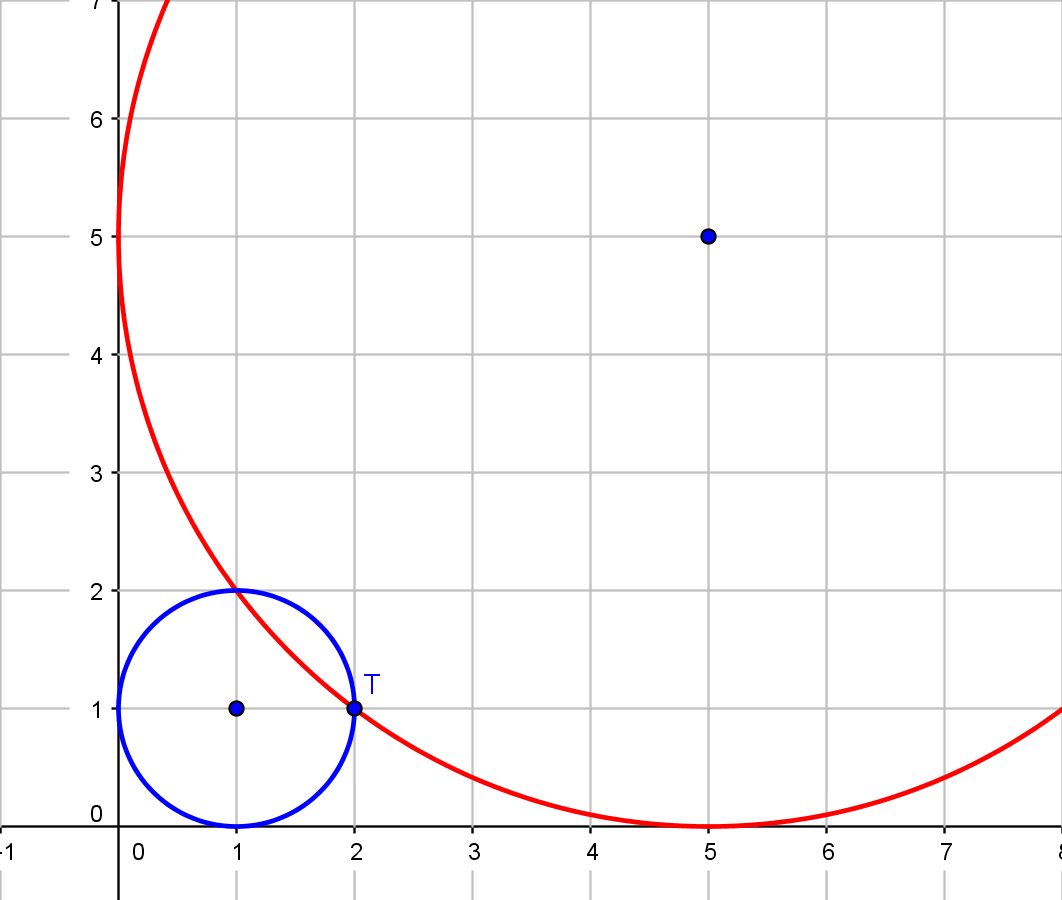
Uočavate li vezu između koordinata središta i polumjera?